Chapter 14 Oscillations

CHAPTER NO.14 OSCILLATIONS

 

14.1 INTRODUCTION

In our daily life we come across various kinds of motions.You have already learnt about some of them, e.g. rectilincar

motion and motion of a projectile. Both these motions are non-repetttive. We have alao learnt about uniform circular

motion and orbital motion of planets in the solar system. In these cases, the motion is repeated after a certain interval of Rime, that is, itis periodic. In your childhood you must have enjoyed rocking in a cradle or swinging on a swing. Both these motions are repetitive in nature but different from the periodic motion of a planet. Here, the object moves to and fro

about a mean position. The pendulum of a wall clock executes a similar motion. Examples of such periodic to and fro motion abound : a boat tossing up and down in a river, the piston in

a steam engine going back and forth, ete. Such a motion is termed as oscillatory motion. In this chapter we study this motion.

 

The study of oscillatory motion is basic to physics; its concepts are required for the understanding of many physical

phenomena. In musical] instruments Hike the sitar, the guitar or the violin, we come across vibrating strings that produce pleasing sounds. The membranes in drums and diaphragms in telephone and speaker systems vibrate to and fro about.their mean positions. The vibrations of air molecules make

the propagation of sound possible. In a sold, the atoms vibrate about their equilibrium positions, the average energy of vibrations being proportional to temperature. AC power stipply give voltage that oscillates alternately going positive and negative about the mean value (ero).

 

The description of a periodic motion in general, and oscillatory motion in particular, requires some fundamental

concepts like period, frequency, displacement, amplitude and phase. These concepts are developed in the next section.

 

14.2 PERKIDEC AND OSCILLATORY MOTIONS

Fig. 14.1 shows some periodic motions. Suppose an insect climbs up a ramp and falls down itt comes back to the initial point and repeats the process identically. If you draw a graph of fta

height above the ground versus time, it would look something like Fig. 14.1 (a). Ifa child climbs up a step, comes down, and repeats the process,its height above the ground would look like that in Fig. 14.1 (b). When you play the game of bouncing a ball off the ground, between your palm and the ground, its height versus time graph would look like the one in Fig. 14.1 (c).Note that both the curved parts in Fig. 14.1 (c)

are sections of a parabola given by the Newton’a equation of motion (gee section 3.6),heut +590 for downward motion, and

1 2 h=ut 99 for upward motion,with different values of u in each case. These are examples of periodic motion. Thus, a motion that repeats ttself at regular intervals of time is called periodic motion.

 

Very often the body undergoing periodic

motion has an equilibrium position somewhere inside its path, When the body is at this position.no net external force acts on it. Therefore, if it ia

left there at rest, it remains there forever. If the body is given a small displacement from the position, a force comes into play which tries to

bring the body back to the equilibrium point,giving rise to osciDations or vibrations. For example, a ball placed in a bowl will be in equilibrium at the bottom. If displaced a little from the point, {t will perform oscillations in the bowl. Every oscillatory motion is pertadic, but.every periodic motion need not be oscillatory.Circular motion is a periodic motion, but it is not oscillatory.

 

There is no significant difference between oscillations and vibrations. It seems that when the frequency is small, we call it oscillation (ike the oscillation ofa branch ofa tree), while when the frequency is high, we call it vibration (like the vibration ofa atring of a musical instrument).

 

Simple harmonic motion is the siuplest form of oscillatory motion. This motion arises when the force on the oscillating body is directly proportional to its displacement from the mean position, which is also the equilibrium position.

Further, at any point in its oscillation, this force is directed towards the mean position.

 

In practice, oscillating bodies eventually come to rest at their equilibrium positions,because of the damping due to friction and other

dissipative causes, However, they can be forced to remain oacillating by means of some external periodic agency. We discuss the phenomena of damped and forced oscillations later in the

chapter.

 

Any material medtum can be pictured as a

collection of a large number of coupled

oscillators. The collective oacillations of the constituents of a medium manifest themselves as waves. Examples of waves include water waves, seismic waves, electromagnetic waves.We shall study the wave phenomenon in the next chapter.

 

14.2.1 Period and frequency We have seen that any motion that repeats itself

at regular intervals of time is called periodic motion. The smallest interval of time after which the motion is repeated is called its period. Let us denote the period by the symbol

T Ttag ST rinit ia second Por nerindic moatons.

 

which are either too fast or too slow on the scale of seconds, other convenient units of time are used. The period of vibrations of'a quartz crystal is expressed in units of microseconds (10° s)abbreviated as 4s. On the other hand, the orbital period of the planet Mercury is 88 earth days.The Halley’s comet appears after every 76 years.The reciprocal of T gives the number of

repetitions that occur per unit time. This quantity is called the frequency of the periodic motion. It is represented by the symbol v. The relation between v and Tis v=l/T (14.1)The unit of v is thus s’. After the discoverer of

radio waves, Heinrich Rudolph Hertz (1857-1894),a specia] name has been given to the unit of frequency. It is called hertz (abbreviated as Hy).

Thus,1 hertz = 1 Hz=1 oscillation per second =1s"!(14.2)Note, that the frequency, v, is not necessarily

an integer.Example 14.2 On an average a human heart is found to beat 75 timea in a minute.Calculate its frequency and period.Answer The beat frequency of heart = 75/(1 min) = 75/(60 s)=1.25s" = 1.25 Hz The time period T =1/0.25 8}

=0.88 <

 

14.2.2 Displacement

In section 4.2, we defined displacement of a particle as the change in its position vector. In this chapter, we use the term displacement in a more general sense. It refers to change with time of any physical property under consideration. For example, in case of rectilinear motion of a steel ball on a surface, the distance from the starting point as a function of time is its position displacement. The choice of origin is a matter of convenience. Consider a block attached to a spring, the other end of which is fixed to a rigid wall [see Fig.14.2(a)]. Generally tt is convenient to measure displacement of the body from its equilibrium position. For an oscillating simple pendulum, the angle from the

vertical as a function of time may be regarded as a displacement variable [see Fig. 14.2(b}]. The term displacement is not always to be referred 

in the context of position only. There can be many other kinds of displacement variables. The voltage across a capacitor, changing with time in an a.c. circuit, is also a displacement

variable. In the same way, pressure variations in time in the propagation of sound wave, the changing electric and magnetic flelda in a ight ‘wave are examples of displacement in different

contexts. The displacement variable may take both positive and negative values. In experiments on oscillations, the displacement is measured for different times.

 

The diaplacement can be represented by a

mathematical function of time. In case of perfodic motion, this function is periodic in time. One of the simplest periodic functions ia given by

S(0 =Acos at (14.3a)If the argument of this function, et, is increased by an integral multiple of 27 radians,the value of the function remains the same. The function f(¢) is then periodic and its period, T,is given by 2 r= (14.3b)

 

Thus, the function fi) is periodic with period T,S10 =f(+T)The same result is obviously correct if we consider a sine function, f(t) = Asin at. Further,

a linear combination of sine and cosine finctions like,SO = Asin ot + Bcos at (14.3c) is also a periodic function with the same period T. Taking,A=Dcos ¢ and B=Dsin¢ Eq. (14.3c) can be written as,

S@ =Dain (at + 9), (14.34)Here Dand ¢ are constant given by D = fa? + B® and o= tan7! (=)

 

The great importance of periodic sine and cosine functions is due to a remarkable result proved by the French mathematician, Jean Baptiste Joseph Fourier (1768-1830): Any periodic function can be expressed as a

superposition of sine and cosine functions of different time periods with suitable coefficients.

 

Example 14.2. Which of the following

functions of time represent (a) periodic and (b) non-periodic motion? Give the period for each case of periodic motion [@ is any positive constant].@) sin af +cos at (i) sin af + cos 2 at + ain 4 at

di) e (tv) log {ad

Answer @ sin at+cos atis a periodic function, it can also be written aa /2 sin (et + 2/4).Now 2 sin (ot +2/4)=2 sin (ot +%/4+2n)= 2 sin [o (t + 2n/a) + x/4]

The periodic time of the function is 21/.

 

(i) This is an example of a periodic motion. It can be noted that each term represents a periodic function with a different angular frequency. Since period is the least interval of time after which a function repeats its

value, ain at has a period T,= 2n/a ; cos 2 wt has a period x/@=T,/2; and sin 4 of has a period 2x/40 = T,/4. The period of the first term is a multiple of the periods of the last two terms. Therefore, the smallest interval

of time after which the sum of the three

terms repeats is T,, and thus the sum is a periodic function with a period 21/a.

 

(ii? The function e“ is not periodic, it

decreases monotonically with increasing

time and tends to zero as t > » and thus,never repeats its value.

 

(iv) The function log{at) increases mono-tonically with time ¢ It, therefore, never Tepeats its value and is a non-periodic function. It may be noted that as t > ~,log(af diverges to ~. It, therefore, cannot represent any Kind of physical displacement.

 

14.3 SIMPLE HARMONIC MOTION

Consider a particle oscillating back and forth about the origin of an x-axis between the limits +A and —Aas shown in Fig, 14.3. This oscillatory motion is said to be simple harmonic if the

displacement x of the particle from the origin varies with time as :x(§ =Acos (t+ § (14.4)where A, mand ¢ are constants.

 

Thus, aimple harmonic motion (SHM) is not any periodic motion but one in which

displacement is a sinusoidal function of time.Fig. 14.4 shows what the positions of a particle executing SHM are at discrete vahie of time, each interval of time being T/4 where T is the period

of motion. Fig. 14.5 plots the graph of xversus f,which gives the values of displacement as a continuous function of time. The quantities A,@and ¢ which characterize a given SHM have

standard names, as summarised in Fig. 14.6.Let us understand these quantities.

The amplitutde A of SHM is the magnitude

of maximum displacement of the particle.

[Note, A can be taken to be positive without any loss of generality). As the cosine function of time variea from +1 to -1, the displacement varies between the extremes A and — A. Two simple harmonic motions may have same @

and ¢ but different amplitudes A and B, as shown in Fig. 14.7 (a).

 

While the amplitude A is fixed for a given SHM, the atate of motion (poattion and velocity)of the particle at any time tis determined by the argument (et + @ in the coaine function. This time-dependent quantity, (at + ¢) is called the phase of the motion. The value of plase at t = 0 is ¢ and is called the phase constant (or phase angle). If the amplitude is known, ¢ can be determined from the displacement at t = 0. Two

simple harmonic motions may have the same A and @ but different phase angle ¢, as shown in Fig. 14.7 (b).

 

Finally, the quantity # can be seen to be related to the period of motion T. Taking, for simplicity, ¢ = 0 in Eq. (14.4), we have xf) = Acos ot (14.5)

Since the motion has a period T, x (4 1s equal to x (t+ T). That is,Acos ot =Acos a(t +T) (14.6)Now the cosine fiinction is periodic with period 2n, Le., it first repeats itself when the argument

changes by 21. Therefore,At +T) = ot + On that is w= 2x/ T (14.7)@ is called the angular frequency of SHM. Ita

S.1. unit ia radiana per second. Since the frequency of oscillations is simply 1/T, @ is 2x times the frequency of oacillation. Two simple harmonic motions may have the same A and 4,but different @, as seen in Fig. 14.8. In this plot

the curve (b) has half the period and twice the frequency of the curve (a).

Example 14.3 Which of the following

functions of time represent (a) aimple

harmonic motion and (b) periodic but not

simple harmonic? Give the pertod for each case.

(1) sin at-—cos at

(2) sin? at

Answer

(a) sin at-cos at

= sin wt— sin (x/2 — ox)

=2 cos (n/4) sin (at- 2/4)

= V2 sin (at - 2/4)

This function represents a simple harmonic motion having a period T = 2n/m and a phase angle (1/4) or (7/4)

(b) sin? at =%-% cos 2 ot

The function is periodic having a period

T= x/o. It also represents a harmonic

motion with the point of equilibrium

occurring at % instead of zero.

 

14,4 SIMPLE HARMONIC MOTION AND

UNIFORM CIRCULAR MOTION

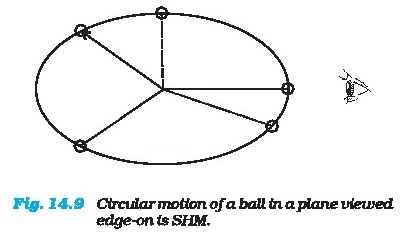
In this section we show that the projection of uniform circular motion on a diameter of the circle follows simple harmonic motion. A simple experiment (Fig. 14.9) helps us visualize

this connection. Tie a ball to the end of a string and make it move in a horizontal plane about a fixed point with a constant angular speed.The ball would then perform a uniform circular

motion in the horizontal plane. Observe the ball sideways or from the front, fixing your attention in the plane of motion. The ball will appear to execute to and fro motion along a horizontal line with the point of rotation as

the midpoint. You could alternatively observe the shadow of the ball on a wall which is perpendicular to the plane of the circle. In this process what we are observing is the motion of the ball on a diameter of the circle normal to the direction of viewing.

 

Fig. 14.10 describes the same situation

mathematically. Suppose a particle P is moving uniformly on a circle of radius A with angular speed ow. The sense of rotation is anticlockwise.The initial position vector of the particle, Le.,

the vector Op at t=0 makes an angle of ¢ with the positive direction of x-axis. In time ¢.

 it will cover a further angle wt and its position vector will make an angle of ot + ¢ with the +ve x axis. Next consider the projection of the position vector OP on the x-axis. This will be OP’. The position of P’ on the x-axis, as the particle P moves on the circle, is given by xf} = Acns (at + ¢)

 

which is the defining equation of SHM. This shows that if P moves uniformly on a circle,its projection P’ on a diameter of the circle executes SHM. The particle P and the circle on which it moves arc sometimes referred to as the reference particle and the reference circle

respectively.

 

We can take projection of the motion of P on any diameter, say the y-axis. In that case, the displacement y(t} of F on the y-axis is given by y= Asin (mt + ¢)

which is also an SHM of the same amplitude as that of the projection on x-axis, but differing by a phase of 2/2.

 

In spite of this connection between circular motion and SHM, the force acting on a particle in Hnear simple harmonic motion is very different from the centripetal force needed to

keep a particle in uniform circular motion.

 

Example 14.4 Fig. 14.10 depicts two

circular motions. The radius of the circle,the period of revolution, the initial position and the sense of revohition are indicated on the figures. Obtain the simple harmonic motions of the x projection of the radius vector of the rotating particle P in each case,

Answer (a) Att=0, OP makes an angle of 45°=2/4 rad with the (positive direction of) x-axis. After time t, it covera an angle 2, in the anticlockwise sense, and makes an angle of 4% with the x-axis.

The projection of OP on the x-axis at time t is given by,x(§ =Acos ( 2 42)

T 4 For T=48,- (Qn on 19 =Acos (=: +4]

which is a SHM of amplitude A, period 4s,and an initial phase’ = ~ .4

(b) In this case at t= 0, OP makes an angle of 90° = ~ with the x-axis. After a time t, it 2 covera an angle of 27, in the clockwise T

 

sense and makes an angle of [z-24)

with the x-axds. The projection of OP on the x-axis at time tis given by

, 22 =Bocos [z-2 at Ey = Bain (27 ,)

T For T= 30 a,a x9 = Bain (=)15)

(nok Whiting this as x(t) = B cos [Zt -2 |, ana comparing with Eq. (14.4). We find that this represents a SHM of amplitude B, period 30s,and an initial phase of -*. <

14.6 VELOCITY AND ACCELERATION IN

SIMPLE HARMONIC MOTION

The speed of a particle v in uniform circular motion is ita angular speed @ times the radius of the circle A.

v=oA (14.8)The direction of velocity > at a time f is along the tangent to the circle at the point where the particle is located at that instant. From the

geometry of Fig. 14.11, it is clear that the velocity of the projection particle P’ at time t ia v(t) = -wA sin (at + ¢) (14.9)

 

where the negative sign shows that o (t) has a direction opposite to the positive direction of x-axis. Eq. (14.9) gives the instantancous velocity of a particle executing SHM, where displacement is given by Eq. (14.4). We can, of course, obtain this equation without using

geometrical] argument, directly by differentiating (Eq. 14.4) with respect of t wll -< x) (14.10)The method of reference circle can be similarly

used for obtaining instantaneous acceleration of a particle undergoing SHM. We know that the centripetal acceleration of a particle P in uniform

circular motion has a magnitude v*/A or oA, and it is directed towards the centre Le., the direction is along PO. The instantaneous acceleration of the projection particle P’ is then

(See Fig. 14.12)a(@ =-aAcos (at+ 9

= wx (A (14.11)Eq. (14.11) gives the acceleration of a particle in SHM. The same equation can again be obtained directly by differentiating velocity v(f)given by Eq. (14.9) with respect to time:alt)=4 vt) (14.12)dt

 

We note from Eq. (14.11) the important

property that acceleration of a particle in SHM is proportional to displacement. For x{Q > 0, a{9 <Oand for x{9 <0, aff > 0. Thus, whatever the value of x between -A and A, the acceleration a{Q is always directed towards the centre.For simplicity, let us put ¢ = 0 and write the expression for x(q, v (0 and até

x8 = Acos wit, v(9 = —« Asin oft, a{=-0* Acos at The corresponding plots are shown in Fig, 14.13.All quantitites vary sinusoidally with time; only their maxima differ and the different plots differ in phase. x varies between -A to A; u{t} varies from —a@A to aA and aff) from —28A to ofA. With respect to displacement plot, velocity plot has a

phase difference of x/2 and acceleration plot has a phase difference of x.

 

Example 14.5 Abody oscillates with SHM

according to the equation (in SI units),

x=5 cos (2x t+ 7/4].Att= 1.58, calculate the (a) displacement,(b) speed and {c) acceleration of the body.

Answer The angular frequency » of the body = 2s" and its time period T= 1 8.

Att=1.58 (a) displacement = (5.0 m) cos [(2x 8" x 153+ 2/4] = (5.0 m) cos [(S2 + #/4)] =-5.0x 0.707 m =-3.535 m

 

(b) Using Eq. (14.9), the speed of the body = — (5.0 m)(@x s°}) sin [((2x s°) x1.5 8 +%/4] =-(5.0 m)(2zs°") sin (Sz+ 2/4)]= 10xx 0.707 ms =22ms*

 

(c) Using Eq.(14.10), the acceleration of the body =-(27 5")? x displacement

=—-(2%5"}? x €3.535 m}=140ms? <

 

14.6 FORCE LAW FOR SIMPLE HARMONIC

MOTION

Using Newton's second law of motion, and the expression for acceleration of a particle undergoing SHM (Eq. 14.11), the force acting on a particle of mass min SHM is F(t) =ma =-mer x(t)te., F(t) =-4x({t) (14.13)where k=mar (14.14a)

k or @ = f (14.14b)m Like acceleration, force is always directed ‘towards the mean position - hence it is sometimes

called the restoring force in SHM. To summarize the discussion so far, simple harmonic motion can be defined in two equivalent ways, either by Eq. (14.4) for displacement or by Eq. (14.13} that

gives tts force law. Going from Eq. (14.4) to Eq. (14.13) required us to differentiate two times.Likewise by integrating the force law Eq. (14.13)

two times, we can get back Eq. (14.4).

 

Note that the force in Eq. (14.13) is linearly proportional to x(4. A particle oscillating under such a force is, therefore, calling a linear harmonic oscillator. In the real world, the force

may contain small additional terms proportional to 22, x, etc. These then are called non-linear oscillators.

 

Exampte 14.6 Two identical springs o:

spring constant k are attached to a block of mass mand to fixed supports as shown ing. 14.14. Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillations.

 

Answer Let the mass be displaced by a small distance x to the right side of the equilibrium position, as shown in Fig. 14.15. Under this situation the spring on the left side gets 

elongated by a length equal to x and that on the right side gets compressed by the same length. The forces acting on the mass are then,F, = -k«x (force exerted by the spring on the left side, trying to pull the mass towards the mean

postition)F, = -kx (force exerted by the apring on the right side, trying to push the mass towards the mean posttian)

 

The net force, F, acting on the maas is then given by,F =-2kx Hence the force acting on the mass ta proportional to the displacement and is directed

towards the mean position; therefore, the motion executed by the mass is simple harmonic. The time period of oscillations is,& T = 2n j— <4 2k

 

14.7 ENERGY IN SIMPLE HARMONIC

MOTION

Both kinetic and potential energies of a particle in SHM vary between zero and their maximum values.In section14.5 we have seen that the velocity of a particle executing SHM, 1s a periodic

function of time. It is zero at the extreme positions of displacement. Therefore, the kinetic energy (K)

of such a particle, which is defined as

K=+ mw? 2 =gm@a sin (at + 9)1 ape

=a k A’sin’ (ex + @) (14.15)is also a periodic function of time, being zero

when the displacement is maximum and

Maximum when the particle is at the mean

position. Note, since the sign of uv is immaterial in K, the period of Kis T/2.

 

What is the potential energy (U) of a particle executing simple harmonic motion? In Chapter 6, we have seen that the concept of potential energy is possible only for conservative forces. The spring force F=-kxis a conservative

force, with associated potential energy

ele U =5* x (14.16)Hence the potential energy of a particle executing simple harmonic motion is,ua = ticx?

2 = sk A? cos(ax + @) (14.17)

 

Thus, the potential energy of a particle

executing simple harmonic motion is also

periodic, with period T/2, being zero at the mean position and maximum at the extreme displacements.It follows from Eqs. (14.15) and (14.17) that the total energy, E, of the system is,E=uU+K

agka cos (at tHt SKA sin’ (at + @)wl 2 2 +2 =gkA [cos (at + ¢) + sin* (at +]

 

Using the familiar trigonometric identity, the value of the expression in the brackets fs unity.Thus,oy,

E= 2 kA (14.18)The total mechanical energy of a harmonic oscillator is thus independent of time as expected for motion under any conservative force. The

thme and displacement dependence of the

potential and kinetic energies ofa linear simple harmonic oscillator are shown in Fig. 14.16.

 

Observe that both kinetic energy and

potential energy in SHM are seen to be always positive in Fig. 14.16. Kinetic energy can, of course, be never negative, since it is proportional to the square of speed. Potential

energy is positive by choice of the undermined constant in potential energy. Both kinetic energy and potential energy peak twice during each period of SHM. For x = 0, the energy is kinetic; at the extremes x = +A, it is all potential

energy. In the course of motion between these Innits, kinetic energy increases at the expense of potential energy or vice-versa.

 

Example 14.7 A block whose mass is 1 kg

is fastened to a spring. The spring has a spring constant of 50 N m7. The block is pulled to a distance x = 10 cm from its equilibrium position at x= 0 on a frictionless surface from rest at t = 0. Calculate the Innetic, potential and total energies of the bleck when it is 5 cm away from the mean position.

Answer The block executes SHM, its angular frequency, as given by Eq. (14.14hb), is o= — m _ f50N m I 1kg

= 7.07 rad s Its displacement at any time t is then given by,xf) = 0.1 cos (7.07%)Therefore, when the particle is 5 cm away from the mean poattion, we have

0.05 =0.1 cos (7.071)Or cos (7.071) = 0.5 and hence 4B sin (7.070) = 4 = 0.868

 

Then, the velocity of the block at x = 5 cm ts =0.1 % 7.07 x 0.866 m s*

=0.61 ms"Hence the KLE. of the block,

zs me 2 = 4[lkg x (0.6123 ms? P|

20.193 The P.E. of the block,=+ kx?

2 = %4(50 N nr x 0.05 m x 0.05 m)

= 0.0625 J The total energy of the block at x= 5 cm,= KE. +P.E.= 0.25 J

 

we also know that at maximum displacement,KE. is zero and hence the total energy of the system is equal to the P.E. Therefore, the total energy of the system, =%(60Nm" x 0.1mx0.1m)

=0.25 J which is same as the sum of the two energies at a displacement of 5 cm. This is in conformity with the principle of conservation ofenergy.

 

14.8 SOME SYSTEMS EXECUTING SIMPLE

HARMONIC MOTION

There are no physical examples of absolutely pure simple harmonic motion. In practice we come across systems that execute simple harmonic motion approximately under certain conditions. In the subsequent part of thia

section, we discuss the motion executed by some such systems.

 

14.8.1 Oscillations dus to a Spring

The simplest observable example of stmple harmonic motion is the small oscillations of a block of mass m fixed to a spring, which in turn is fixed to a rigid wall as shown in Fig. 14.17.

The block is placed on a frictionless horizontal surface. If the block is pulled on one side and is rekased, it then executes a to and fro motion

about a mean position. Let x = 0, indicate the position of the centre of the block when the

 spring is in equilibrium. The positions marked

as -A and +A indicate the maximum

displacements to the left and the right of the Mean position. We have already learnt that springs have special properties, which were first

discovered by the English physicist Robert Hooke. He had shown that such a system when deformed, is subject to a restoring force, the Magnitude of which is proportional to the deformation or the displacement and acts in opposite direction. This is known as Hooke's

law (Chapter 9). It holds good for displacements small in comparison to the length of the spring.At any time f, if the displacement of the block from its mean position is x, the restoring force F acting on the block is,FQ) =-kx (14.19) The constant of proportionality, k, is called the spring constant, its value is governed by the elastic properties of the spring. A stiff spring has large k and a soft spring has small k. Equation (14.19) is same aa the force law for SHM and therefore the system executes a simple harmonic motion. From Eq. (14.14) we have,@ = fe (14.20)

m and the period, T, of the oscillator is given by,T=2 nfm (14.21)Stiff springs have high value of k (spring constant). A block of small mass m attached to

a stiff spring will have, according to Eq. (14.20),large oscillation frequency, as expected physically.

 

 

Example 14.8 A5 kg collar is attached to a spring of spring constant 500 N nor?. It slides without friction over a horizontal rod.The collar is displaced from its equilibrhim position by 10.0 cm and released. Calculate

(a) the period of oscillation,

(b} the maxtmum speed and

(c) maxtmum acceleration of the collar.

Answer (a) The period of oscillation as given by Eq. (14.21) is,, _[5.0ke

= Mm =O, |——-> — Ts anf TOON = (2%/10) s

= 0.63 s (b) The velocity of the collar executing SHM is given by,ult) = Am sin (at + ¢)The maximum speed is given by,

v= Aw k =0.1x fe m 500N m7!=0.1 x j————

5kg =lms' and it occurs at x= 0

 

(c) The acceleration of the collar at the displacement x (#) from the equilibrium is given by,ald = -o x6

‘k =—-— x(t)m Therefore the maximum acceleration is, ggg = OP A , -1

= SOON m xQ.1m 5 kg =10ms and it occurs at the extremities.

 

14.8.2 The Simple Pendulum

It is said that Galileo measured the periods of a swinging chandelier in a church by his pulse beats. He observed that the motion of the chandelier was periodic. The system is a kind of pendulum. You can also make your own

pendulum by tying a piece of stone to a long unstretchable thread, approximately 100 cm long. Suspend your pendulum from a suitable support so that it is free to oscillate. Displace the stone to one side by a amall distance and let tt go. The stone executes a to and fro motion,

itis periodic with a period of about two seconds.

 

We shall show that this periodic motion is simple harmonic for small displacements from the mean position. Consider simple pendulum —a small boh of mass m tied to an inextensible

mass less string of length L. The other end of the string is fixed to a support in the cefling.The bob oscillates in a plane about the vertical line through the support. Fig. 14.18(a) shows

this system. Fig. 14.18(b) is a kind of ‘free-body’diagram of the simple pendulum showing the forces acting on the bob.

 

Let @ be the angle made by the string with the vertical. When the bob is at the mean position, 8=0

 

There are only two forces acting on the bab;the tension T along the string and the vertical force due to gravity (=mg). The force mg can be resolved into the component mg cos6 along the string and mg sin perpendicular to it. Since

the motion of the bob is along a circle of length Land centre at the support point, the bob has a radial acceleration (@*1) and also a tangental acceleration; the latter arises since motion along

the arc of the circle is not uniform. The radial acceleration is provided by the net radial force T-mg cos@, while the tangential acceleration is

provided by mg sin®@. It is more convenient to work with torque about the support since the radial force gives zero torque. Torque 7 about the support is entirely provided by the tangental

component of force t= -L(mgainé) (14.22)

This is a restoring torque that tends to reduce angular displacement — hence the negative sign. By Newton's law of rotational motion,t=le (14.23)where I is the moment of inertia of the system

about the support and « is the angular

acceleration. Thus,Ia=-mgsinéd L (14.24)

Or,, mgLl.a= -—— sine (14.25)

 

We can simplify Eq. (14.25) if we assume that the displacement @is small. We know that sin @ can be expressed as,sin@ = g-F+Es.. (14.26)where @ {a in radians.

Now if 6 is small, sin 6can be approximated by @ and Eq. (14.25) can then be written as,, mgL a= “|? (14.27)

In Table 14.1, we have listed the angle @ in degrees, its equivalent in radians, and the value SHM - how small should the amplitude be? When you perform the experiment to determine the time period of a simple  pendulum, your teacher tells you to keep the amplitude small. But have you ever asked how small is small? Should the amplitude to 5°, 2° 1° or 0.5°? Or could it be 10°, 20° or 30°7

 

To appreciate this, it would be better to measure the time period for different

amplitudes, up to large amplitudes. Of

course, for large oscillations, you will have to take care that the pendulum oscillates in a vertical plane. Let us denote the time period for small-amplitude oscillations as TO) and write the time period for amplitude 0, a8 116,) = cT (0), where cis the multiplying factor. If you plot a graph of ¢ versus 9,you will get values somewhat like this:

@% 3 2° =645° «= 50° 70° 90°

eo: 1.02 1.04 105 1.10 1.18

 

This means that the error in the time

period ia about 2% at an amplitude of 20°,5% at an amplitude of 50°, and 10% at an amplitude of 70° and 18% at an amplitude of 80°.In the experiment, you will never be able to measure T (0) because this means there are no oscillations. Even theoretically,

sin @ is exactly equal to 6 only for 6 = 0.There will be some inaccuracy for all other values of 6 . The difference increases with increasing 6. Therefore we have to decide how much error we can tolerate. No measurement is ever perfectly accurate.You must also consider questions like these: What is the accuracy of the stopwatch? What is your own accuracy in starting and stopping the stopwatch? You will realise that the accuracy in your Measurements at this level is never better than 5% or 10%. Since the above table shows that the time period of the pendulum increases hardly by 5% at an amplitude of 50° over its low amplitude value, you could very well keep the amplitude to be 50° in your experiments.of the function ain @ . From this table it can be

seen that for @ as large as 20 degrees, ain 6 is nearly the same as @ expressed in radians.Table 14.1 sin (as « function of angle 6 Equation (14.27) is mathematically, identical to Eq. (14.11) except that the variable is angular

displacement. Hence we have proved that for small 0, the motion of the bob ts simple harmonic.From Eqs. (14.27) and (14.11),a= nigh I and T =2a tT (14.28)

mgL .Now since the string of the simple pendulum is mass leas, the moment of inertia I is simply mL?, Eq. (14.28) then gives the well-known formula for time period of a simple pendulum.

L T= an fe (14.29)g

 

Example 14.9 What is the length of a

simple penduhm, which ticks seconds ?

Answer From Eq. (14.29), the time period of a simple pendulum ts gtven by.

T= 2" f g From this relation one gets,

po 4n The time period of a simple pendulum, which ticks seconds, is 2 s. Therefore, for g = 9.8 ms?

and T =2a, Lis _ 9.8m s*) x A(s*)

An® =lm <

 

 

14.9 DAMPED SIMPLE HARMONIC MOTION

We know that the motion ofa simple pendulum,swinging in air, dies out eventually. Why does it happen ? This is because the air drag and the friction at the support oppose the motion of the

pendulum and dissipate its energy gradually.The pendulum is said to execute damped eacillations. In dampled oscillations, the energy of the system is dissipated continuously; but,

for small damping, the oscillations remain approximately periodic. The dissipating forces are generally the frictional forces. To understand

the effect of such external forces on the motion of an oscillator, let us consider a system as shown in Fig. 14.19. Here a block of mass m

connected to an elastic spring of spring constant k oscillates vertically. If the block is pushed down a little and released, ita angular frequency of

oscillation is © = fe . a9 seen in Eq. (14.20).However, in practice, the surrounding medium (air) will exert a damping force on the motion of

the block and the mechanical energy of the block-spring system will decrease. The energy loss will appear as heat of the surrounding medtum {and the block also) [Fig. 14.19].

 

The damping force depends on the nature of the surrounding medium. If the block is immersed in a liquid, the magnitude of damping will be much greater and the dissipation of energy much faster. The damping force is generally proportional to velocity of the bob.[Remember Stokes’ Law, Eq. {10.19)] and acts opposite to the direction of velocity. If the

damping force is denoted by F,, we have

F, =-bv (14.30)where the positive constant b depends on characteristics of the medium (viscosity, for example} and the size and shape of the block,

ete. Eq. (14.30) is usually valid only for small veloctty.

 

When the mass m is attached to the spring and released, the spring will elongate a little and the mass wil setile at some height. This position,

shown by © in Fig 14.20, is the equilibrium position of the mass. If the mass is pulled down or pushed up a Hitile, the restoring force on the

block due to the spring is F, = -kx, where z is the displacement* of the mass from its equilibrium position. Thus, the total force acting on the mass at any time ¢, is F = -4cx -bv.

 

If aft) is the acceleration of mass at time t,then by Newton's Law of Motion applied along the direction of motion, we have malt) =-k xt) - b uf) (14.31)

Here we have dropped the vector notation

because we are discussing one-dimensional motion.Using the first and second derivatives of x (0 for v (6 and a (6 respectively, we have mix pXskx=0 (14.32)dt“ ct

 

The solution of Eq. (14.32) describes the motion of the block under the influence of a damping force which is proportional to velocity.The solution is found to be of the form xQ = Ae>#a cop (wt + 6) (14.33)where ais the amplitude and m’ is the angular frequency of the damped oscillator given by,os few (14.34) mo 4°

 

In this function, the cosine function has a period 2x/a! but the function 2{¢) is not strictly periodic because of the factor e? “"™ which decreases  ontinuously with time. However, if the

decrease is amall tn one time period T, the motion Tepresented by Eq. (14.33) is approximately periodic.

 

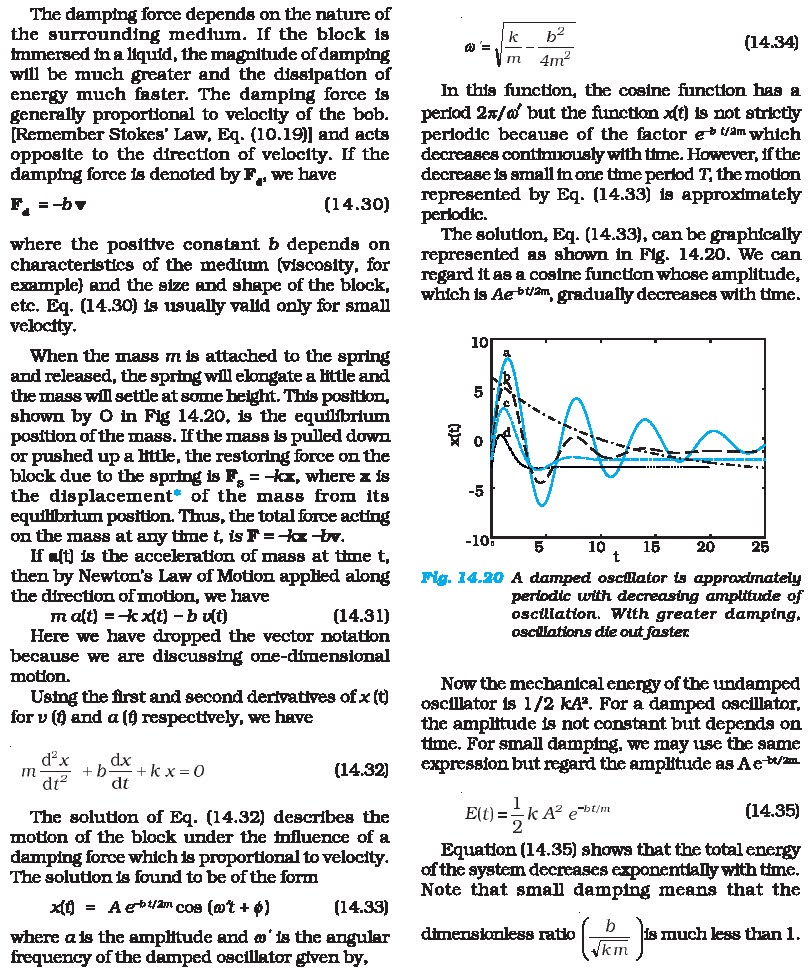
The solution, Eq. (14.33), can be graphically Tepresented as shown in Fig. 14.20. We can Tegard it as a cosine function whose amplitude,which is Ae?¥2™, gradually decreases with time.

 

Now the mechanical energy of the undamped oscillator is 1/2 kA®. For a damped oscillator,the amplitude is not constant but depends on time. For small damping, we may use the same expression but regard the amplitude as Ae =

El) = = kc A? eet (14.35)

 

Equation (14.35) shows that the total energy of the system decreases exponentially with time.Note that small damping means that the dimensionless ratio (—?_ |is much less than 1.

vkm Of course, an expected, if we put b = 0, all equations of a damped oscillator in this section reduce to the corresponding equations of an undamped oscillator.

 

Example 14.10 For the damped oscillator

shown in Fig. 14.20, the mass m of the block is 200 g, k = 90 N nor’ and the damping constant b is 40 g s7. Calculate (a) the period of oscillation, (b) time taken for its amplHtude of vibrations to drop to half of its inttial value and (c) the time taken for its mechanical energy to drop to half its initial value.

Answer (a) We see that kn = 90x0.2 = 18 kg N or'= kg* s*; therefore Ji, = 4.243 kg s1, and b = 0.04 kg s"!. Therefore b is much less than ‘Jim - Hence the time period T from Eq. (14.34)is given by

T= anf k on 0.2 kg 90 N m*! = 038

 

(b) Now, from Eq. (14.33), the time, T, ,. for the amplitude to drop to half of ite initial value is given by, t _In1/2)

”“ b/2m = 0-698 , 2x200 s 40 = 6.93 8

 

(c) For calculating the time, ¢,,,, for its mechanical energy to drop to half ite initial value we make use of Eq. (14.35). From this equation ‘we have,

E(t, J/E@) = exp (dt,,,/m Or % = exp (tt,,,/m In (1/2) = ~{bt,,./m)

0.693 Or bia = 40g 57 x 200 g

= 3.46s

 

This ia just half of the decay period for amplttude. This is not surprising, because,according to Eqs. (14.33) and (14.35), energy depends on the square of the amplitude. Notice that there ia a factor of 2 in the exponents of

the two exponentials.

 

14.16 FORCED OSCILLATIONS AND

RESONANCE

When a system (such as a simple pendulum or a block attached to a spring) is displaced from its equilibrium position and released, it oscillates with its natural frequency @, and the cacillations are called free oscillations. All free oscillations

eventually die out because of the ever present damping forces. However, an external agency can maintain these oacillations. These are called

force or driven oscillations. We consider the case when the external force is itself periodic,with a frequency «, called the driven frequency.A most important fact of forced periodic oscillations is that the system oscillates not with its natural frequency @, but at the frequency @,

of the external agency; the free oscillations die out due to damping. A moat familiar example of forced oscillation is when a child in a garden

swing periodically presses his feet against the ground (or someone else periodically gives the child a push) to maintain the oscillations.

 

Suppose an external force Ff) of amplitude F, that varies periodically with time is applied to a damped oscillator. Such a force can be

Tepresented as,Fi) =F, cos o,¢ (14.36)

The motion of a particle under the combined action of a linear restoring force, damping force and a time dependent driving force represented

by Eq. (14.36) ta given by,maft) = -k x(t) — bu{t) + F,cos@,t (14.37a)

Substituting d?x/d@ for acceleration in

Eq. (14.37a} and rearranging it, we get

Px) dx _ "ae? brag t kx= F, cos o,t (14.376)

 

This is the equation of an oscillator of mass m on which a periodic force of (angular)frequency ,1s applied. The oscillator initially oscillates with its natural frequency # When we apply the external periodic force, the oscillations with the natural frequency die out,and then the body oscillates with the (angular)frequency of the external periodic force. lta  displacement, after the natural oscillations die out, is given by

aff) = Acos (m,t + ¢) (14.38)where tis the time measured from the moment when we apply the periodic force.

 

The amplitude A is a function of the forced frequency @, and the natural frequency o.Analysis shows that it is given by F A ——_——ar {mm (o* -@) +o% b'| (14.394)=o and tan¢= @,X, (14.39b)where m is the mass of the particle and v, and

x, are the velocity and the displacement of the particle at time t= 0, which is the moment when.we apply the periodic force. Equation (14.39)shows that the amplitude of the forced oscillator

depends on the (angular) frequency of the driving force. We can see a different behaviour of the oscillator when o, is far from wand when it is close to w. We consider these two cases.

(a) Small Damping, Driving Frequency far

from Natural Frequency : In this case, o,b will be much smaller than m(’-o), and we can neglect that term. Then Eq. (14.39) reduces to F As (14.40)m | Oo -— Oo ]

 

Fig. 14.21 shows the dependence of the

displacement amplitude of an oscillator on the angular frequency of the driving force for different amounts of damping present in the system. It may be noted that in all the cases the amplitude is greatest when @, /= 1. The curves

in this figure show that smaller the damping,the taller and narrower ts the resonance peak.

if we go on changing the driving frequency,the amplitude tends to infinity when it equals the natural frequency. But this is the ideal case

of zero damping, a case which never arises ina real system as the damping is never perfectly zero. You must have experienced in a swing that when the timing of your push exactly matches

with the time period of the swing, your swing gets the maximum amplitude. This amplitude is large, but uot infinity, because there is always some damping in your swing. This will become clear in the (b).

 

(b) Driving Frequency Close to Natural

Frequency :If @, is very close to a, m (a? -w;)} would be much less than o, 5, for any reasonable value of b, then Eg. (14.39) reduces ta Ass. (14.41)a,b

 

This makes it clear that the maximum

possible amplitude for a given driving frequency is governed by the driving frequency and the damping, and is never infinity. The phenomenon of increase in amplitude when the driving force

is close to the natural frequency of the oscillator is called resonance.

 

In our daily life we encounter phenomena

which involve resonance. Your experience with swings is a good example of resonance. You might have realised that the skill in swinging te greater heights lies in the synchronisation of the rhythm of pushing against the ground with the natural frequency of the swing.

To illustrate this point further, let us

consider a set of five simple pendulums of assarted lengths suspended from a common rope as shown in Fig. 14.22. The pendulums 1 and 4 have the same lengths and the others have different lengths. Now let us set penduhmn into

motion. The energy from this pendulum gets transferred to other pendulums through the connecting rope and they start oscillating. The driving force is provided through the connecting

rope. The frequency of this force is the frequency with which pendulum oscillates. If we observe the response of pendulums 2, 3 and 5, they frst

start oscillating with their natural frequencies of oscillations and different amplitudes, but this

motion is gradually damped and not sustained.Their frequencies of oscillation gradually change and ulthmately they oscillate with the

frequency of pendulum 1, Le. the frequency of the driving force but with different amplitudes.They oscillate with small amplitudes. The response of pendulum 4 is in contrast to this

set of penduluns. It oscillates with the same frequency as that of pendulum 1 and its amplitude gradually picks up and becomes very large. A resonance-like response is seen. This happens because in this the condition for resonance is satisfied, Le. the natural frequency

of the system coincides with that of the driving force.

 

We have so far considered oscillating systems which have just one natural frequency. In general, a system may have several natural frequencies. You will see examples of such systems (vibrating strings, air cohumns, etc.) in the next chapter. Any mechanical structure, Hike

a building, a bridge, or an aircraft may have several possible natural frequencies. An external periodic force or disturbance will set the system in forced oscillation. If, accidentally,

the forced frequency , happens to be close to one of the natural frequencies of the system,the amplitude of oscillation will shoot up{(resonance), resulting in possible damage. This

is why soldiers go out of step while crossing a bridge. For the same reason, an earthquake will not cause uniform damage to all building in an affected area, even if they are built with the

same strength and materials. The natural

frequencies of a building depend on tts height,and other size parameters, and the nature of building materials. The one with {ts natural frequency close to the frequency of seismic wave in likely to be damaged more.

 

SUMMARY

1. The motions which repeat themselves are called periodic motions.

 

2. The period Tis the time required for one complete oscillation, or cycle. It ia related to the frequency v by,

T= i v The frequency v of periodic or oscillatory motion is the number of oscillations per unit time. In the SI, it is measured in hertz :1 hertz = 1 Hz = 1 oscillation per second = 1s”

 

3. In simple  harmonic motion (SHM), the displacement x (§ of a particle from its equilibrium posttion ie given by,x(@ =Acos  (at+¢) (displacement},im which A is the amplitude of the displacement, the quantity (at +¢) is the phase of the motion, and ¢ is the phase constant. The angular frequency is related to the

period and frequency of the motion by,

, 2a Oa = 2zv fangular frequency}.

 

4. Stmple harmonic motion is the projection of uniform circular motion on the diameter of the circle in which the latter motion occurs.

 

5, The particle velocity and acceleration during SHM as functions of time are given by,v(O = -mA sin (ot + ¢)} {velocity},a(Q = -aA cos (at+ 6}

= -wx (4 (acceleration),Thus we see that both velocity and acceleration of a body executing atmple harmonic motion are periodic functions, having the velocity amplitude v.=a@ A and acceleration

amplitude a, =A, respectively.

 

6. The force acting simple harmonic motion is proportional to the displacement and ia always directed towarda the centre of motion.

 

7. A particle executing simple harmonic motion has, at any time, kinetic energy

K= % aw* and potential energy U = % ké, If no friction is present the mechanical

energy of the system, E = K + U alwaya remains conatant even though K and Uchange with time,

 

8. A particle of mase m oacillating under the influence of a Hooke’s law restoring force given by F =— kx exhibits stmple harmonic motion with

fk o= im (angular frequency}T= anf (period)Such a system is also called a linear oscillator.

 

9. The motion of a simple pendulum swinging through small angles is approximately simple harmonic, The period of oscillation is given by,

T= aft g

 

10. Themechanical energy in a real oscillating system decreases during oscillations because external forces, such as drag, inhibit the oscillations and transfer mechanical energy

to thermal energy. The real oscillator and its motion are then said to be damped. If the damping force ia given by F,, = -bv, where v is the velocity of the oscillator and bis a damping constant, then the displacement of the oacillator is given by,(0 = Act cog (xt + 9} where oy’, the angular frequency of the damped oacillator, 1a given by

wo = §—-—z m 4Am* If the damping conetant ie small then w’~ « where « is the angular frequency of the undamped oscillator. The mechanical energy E of the damped oacillator is given by

E(t) = 1 azemim 2

 

11. fan external force with angular frequency @, acts on an oscillating system with natural angular frequency , the system oscillates with angular frequency , The amplitude of  oscillations is the greatest when

o, =o a condition called resonance.

 

POINTS TO PONDER

1. The period Tia the tenst time after which motion repeata fteclf. Thus, motion repeats itself after nT where n ia an integer.

 

2. Every periodic motion is not simple harmonic motion. Only that pericdic motion governed by the force law F = —k xis simple harmonic.

 

3. Circular motion can arise duc to an inverse-square law force (as in planetary motion)as well as duc to simple harmonic force in two dimensions equal to: ner, In the latter case, the phases of motion, in two perpendicular directions (x and 13 must differ

by /2. Thus, a particle subject to a force —imerr with initial position (o, A) and velocity (aA, 0) will move uniformly in a circle of radius A.

 

4. For linear simple harmonic motion with a given two arbitrary initia] condtftions are necessary and sufficient to determine the motion completely. The mitial conditian may be () inftial posttion and initial velocity or (i) amplinude and phase or [tii) energy

and phase.

 

5. From point 4 above, given amplitude or cuergy, phase of motion ia determined by the initial position or initial velocity.

 

6. A combination of two simple harmonic motions with arbitrary amplitudes and phases is not necessarily periodic. It is periodic only if frequency of one motion fs an integral multiple of the other’s frequency. However, a periodic motion can always be expressed as a sum of infinite number of hanmonic motions with appropriate amplitudes.

 

7, The period of SHM doea not depend on amplitude or energy or the phase constant.Contrast this with the periods of planetary orbits under gravitation (Kepler's third law).

 

8. The motion of a simple pendulum is simple harmonic for anall angular displacement.

 

9. For motion of a particle to be aimple harmonic, its displacement x must be expressible in either of the following forms :x=Acos at + Basin at x=Acos (at+a),x= Basin (at+ §)

 

The three forms are completely equivalent (any one can be expresaed in terms of any other two forms).Thus, damped simple harmonic motion (Eq. (14.31)] 16 not strictly simple harmonic. It is approximately so only for time intervala much less than 2m/b where bis the damping constant.

 

10. In forced oscillations, the steady state motion of the particic (after the force oscillations dic out) is simple hanmonic motion whose frequency is the frequency of the driving frequency @, not the natural frequency of the particic.

 

11. In the ideal case of zero daurping, the amplitude of simple harmonic motion at resonance is infinite. This is no problem since all real systems have some damping, however,ammall.

 

12. Under forced oscillation, the phase of harmonic motion of the particle differs from the phase of the driving force.

 

Exercises

14.1 Which of the following examples represent periodic motion?

a) Aaswimmer completing one (return) trip from one bank of a river to the other and back.

 

(b) A freely suspended bar magnet displaced from ita N-S direction and released.

 

(c) Abydrogen molecule rotating about its centre of mass.

 

(d) An arrow released from a bow.

 

14.2 Which of the following examples represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?

(a) = the rotation of earth about its axis.

(b) =motion of an oscillating mercury column in a U-tube.

(c) motion of a ball bearing inaide a smooth curved bowl, when released from a

point slightly above the lower most point.

(d = general vibrations of a polyatomic molecule about its equilibrium positian.

 

14.3 Fig. 14.28 depicts four st plots for linear motion of a particle. Which of the plots represent periodic motion? What is the period of motion (in case of periodic motion) ?

 

14.4 Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (# is any positive constant):

(a) ain wt —coa at

(b) ain? at

(c} 3 cos (x/4- 208

(d) cos at + cos Sat + cos Sat

(e} = exp (044 ® l+at+ wf

 

14.6 Aparticle ie in lincar ample harmonic motion between two paints, A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signe of velocity, acceleration and force on the particle when it is

a) atthe endA,

b) at the end B,

(c} at the mid-point of AB going towards A,

(d) at 2 cm away from B going towards A,

(e} at 3 cm away from A going towarde B. and at 4cm away from B going towards A.

 

14.6 Which of the following relationships between the acceleration aand the displacement x of a particle involve simple harmonic motion?

(a) an0.7x

(b) =a=-200%

(c) a=-10x

(d) a=100%

 

14.7 The motion of a particle executing simple harmonic motion is described by the displacement function,48 = A coa (at + ¢}.If the initial (t = 0} position of the particle is 1 cm and its initial velocity is @ cm/s,what are its amplitude and initial phase angle ? The angular frequency of the particle is 1 5". If instead of the cosine function, we choose the sine function to describe the SHM : x= B sin (#t + a, what are the amplitude and initial phase of the

particle with the above initial conditions.

 

14.8 Aspring balance hae a scale that reade from 0 to 50 kg. The length of the acale is 20 cm. A body euspended from thia balance, when displaced and released, orgcillates with a period of 0.6 s. What is the weight of the body ?

 

14.9 A spring having with a epring constant 1200 N m™ ts mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The maas is then pulled sideways to a distance of 2.0 cm and released.Determine (f) the frequency of oacilations, (ii) maximum acceleration of the mass,and (iii) the maximum speed of the mass.

 

14.10 In Exercise 14.9, let us take the poaition of mass when the spring is unstreched as x = 0, and the direction from left to right aa the positive direction of x-axis. Give x as a function of time é for the oacillating mans if at the moment we start the stopwatch (t = 0), the masa is

(a) at the mean position,

(b) at the maxtmum stretched position, and

(c) at the maximum compregsed position.

In what way do these functions for SHM differ from each other, in frequency, in

amplitude or the initial phase?

 

14.11 Figures 14,25 correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revohition (.c. clockwise or anti-clockwise) are indicated on each figure.

Obtain the corresponding aimple harmonic motions of the x-projection of the radius vector of the revolving particle P, in each case.

 

14.13 Plot the corresponding reference circle for each of the following simple harmonic motiona. Indicate the initial (¢ =0) position of the particle, the radius of the circle,and the angular speed of the rotating particle. For simplicity, the sense of rotation

may be fixed to be anticlockwise in every case: (x 1s in cm and tis in s),

(a) x= -2 ain (St+ 7/3)

(b) x= cos (x/6-§

(c} x= ain (axt+ 7/4)

(d) x=2 cos at

 

14.19 Figure 14.26 (a) ahows a spring of force constant k clamped rigidly at one end and & mass m attached to ite free end. A force F applied at the free end stretches the apring. Figure 14.26 (b) shows the same spring with both ends free and attached to a maga mat either end. Each end of the spring in Fig. 14.26(b) is stretched by the aame force F.

 

(a) What is the maximum extenaion of the spring in the two cases 27 tb) = if the maga in Fig. (a) and the two maases in Fig. (b) are released, what is the

period of oscillation in each case ?

 

14.14 The piston in the cylinder head of a locomotive has a stroke (twice the amplitude)of 1.0m. Ifthe piston moves with simple harmonic motion with an angular frequency of 200 rad/min, what is ite maximum speed ?

 

14.15 The acceleration due to gravity on the surface of moon is 1.7 m s*. What is the time period of a simple pendulum on the surface of moon if its time period an the surface of earth is 3.5 a ? (g on the surface of earth ia 9.8 m s4}

 

14.16 Answer the following questions :

(a) Time period of a particle in SHM depends on the force constant k and mass m of the particle:T= an. A shmple pendulum executes SHM approximately. Why then is k the time period of a pendulum independent of the mass of the pendulum?

 

(b) ~The motion of a simple pendulum is approximately simple harmonic for small

angle oscillations. For larger angles of oscillation, a more involved analysis

7 fl shows that T is greater than anf Think of a qualitative argument to

g appreciate this result.

 

(c} Aman with a wristwatch on his hand falls from the top of a tower. Does the

watch give correct time during the free fall ?

 

d) What is the frequency of oscillation of a simple pendulum mounted in a cabin

that is freely falling under gravity ?

 

14.17 Asimple pendulum of length { and having a bob of mase M is suspended in a car.The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be ite time period ?

 

14.18 Acylindrical piece of cork of denaity of base area A and height h floats in a liquid of density p, The cork is depressed alightly and then released, Show that the cork

oacillatea up and down simple harmonically with a period . ip T = 22 [— AG where p is the density of cork. (ignore damping due to viscosity of the liquid).

 

14.19 One end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference ia maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.

 

Additional Exercises

14.20 An air chamber of volume V has a neck area of cross section a into which a ball of mass m just fite and can move up and down without any friction (Fig. 14.27). Show that when the ball is pressed down a little and released . it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].

 

14.21 You are riding in an automobile of mass 3000 kg. Assuming that you are examining the oscillation  characteristice of its suspension system. The suspension sags 15 aan when the entire automobile ta placed on it. Also, the amplitude of oscillation decreases by 50% during one complete oscillation. Estimate the values of (a) the spring constant kand (b) the damping constant b for the spring and shock absorber system of one wheel, assuming that each wheel supports 750 kg.

 

14.22 Show that for a particle in linear SHM the average kinetic energy over a period of oscillation equals the average potential energy over the same period.

 

14.23 Acircular disc of masa 10 kg is suspended by a wire attached to its centre. The wire is twisted by rotating the disc and released. The period of toraional oscillations is found to be 1.5 a. The radius of the disc is 15 cm. Determine the torsional spring constant of the wire. (Torsional spring constant a is defined by the relation J=-a6, where Jia the restoring couple and @ the angle of twist).

 

14.24 Abody deacribes simple harmonic motion with an amplitude of 5 cm and a period of 0.2 ». Find the acceleration and velocity of the body when the displacement ia (a) 5 cm (b) 8 cm (c} O cm.

 

14.25 Amase attached to a apring ia free to oacillate, with angular velocity @, in a horizontal plane without friction or damping. It is pulled to a distance x, and pushed towarde the centre with a velocity v, at time t= 0, Determine the amplitude of the resulting oscillations in terms of the parameters o, *, and v,, [Hint ; Start with the equation

<= 2. con (wé+6) and note that the initial velocity is negative.]

 

In solids, similar arguments can be made. In a crystalline solid, atoms or group of atoms are arranged in a periodic lattice. In these, each

atom or group of atoms is in equilibrium, due to forces from the surrounding atoms. Displacing

one atom, keeping the othera fixed, leada to restoring forces, exactly as in a spring. So we can think of atoms in a lattice as end points,with springs between pairs of them.In the anbsequent sections of this chapter we are going to discuss various characteristic

properties of waves.

 

15.2 TRANSVERSE AND LONGITUDINAL

WAVES

We have seen that motion of mechanical waves involves oscillations of constituents of the medium. If the constituents of the medium oscillate perpendicular to the direction of wave

propagation, we call the wave a transverse wave.If they oscillate along the direction of wave propagation, we call the wave a longitudinal wave.

 

Fig.15.2 shows the propagation of a single pulse along a string, resulting from a single up and down jerk. If the string is very long compared to the size of the pulse, the pulse will damp out

before it reaches the other end and reflection from that end may be ignored. Fig. 15.3 ahows a similar situation, but this time the external agent gives a continuous periodic sinusoidal 1p

and down jerk to one end of the string. The resulting disturbance on the string ‘s then a sinusoidal wave. In either case the elements of the string oscillate about their equilibrium mean.