Chapter 3 Motion And A Straight Line
CHAPTER NO.3 MOTION IN A STRAIGHT LINE
3.1 INTRODUCTION
Motion is common to everything in the universe. We
walk,run and ride a bicycle. Even when we are sleeping, air moves into and out
of our lungs and blood flows in arteries and veins. We see leaves falling from
trees and water flowing down a dam. Automobiles and planes carry people from
one place to the other. The earth rotates ance every twenty-four hours and
revolves round the sun once in a year. The sun itself is in motion in the Milky
Way, which is again moving within its local group of galaxies.
Motion ts change in position of an object with time.
How does the position change with time ? In this chapter, we shall learn how to
describe motion. For this, we develop the concepts of velocity and
acceleration. We shall confine ourselves to the study of motion of objects
along a straight line, alao known as rectilinear motion. For the case of
rectilinear motion with uniform acceleration, a set of simple equations can be
obtained. Finally, to understand the relative nature of motion, we introduce
the concept of relative velocity.
In our discussions, we shall treat the objects in
motion as point objects. This approximation is valid so far as the size of the
object is much smaller than the distance it moves ina reasonable duration of
time. Ina good number of situations in real-life, the size of objects can be
neglected and they can
be considered as point-like objects without much
error.
In Kinematics, we study ways to describe motion
without going into the causes of motion. What causes motion deacribed in this
chapter and the next chapter forms the subject matter of Chapter 5.
3.2 POSITION, PATH LENGTH AND
DISPLACEMENT
Earlier you learnt that motion is change in position
of an object with time. In order to specify position, we need to use a
reference point and a set of axes. It is convenient to choose a rectangular
coordinate system consisting of
three mutually perpenducular axes, labelled X-,Y-,
and Z- axes. The point of intersection of these three axes is called origin (O)
and serves as the
reference point. The coordinates (x, y. z) of an
Object describe the position of the object with Tespect to this coordinate
system. To measure
time, we position a clock in this system. This
coordinate system along with a clock constitutes a frame of reference.
Ifone or more coordinates ofan object change with
time, we say that the object is in motion.Otherwise, the object is aaid to be
at reat with respect to this frame of reference.
The choice of a set of axes in a frame of Teference
depends upon the sitmation. For example, for describing motion in one
dimension,we need only one axis. To describe motion in two/three dimensions, we
need a set of two/three axes.
Description of an event depends on the frame of
reference chosen for the deacription. For example, when you say that a car is
moving on a road, you are describing the car with respect
to a frame of reference attached to you or to the
ground. But with respect to a frame of reference attached with a person sitting
in the car, the
car is at rest.
To describe motion along a atraight line, we can
choose an axis, say X-axia, 30 that it coincides with the path of the object.
We then measure the position of the object with reference to a conveniently
chosen origin, say O, as shown in Fig. 3.1. Positions to the right of O are
taken as positive and to the left of O, as negative.Following this convention,
the position
coordinates of point P and Q in Fig. 3.1 are +360
mand +240 m. Similarly, the position coordinate of point R is -120 m.
Path tength
Consider the motion of a car along a straight Ine.
We choose the x-axis such that it coincides with the path of the car’s motion
and origin of the axis as the point from where the car started
moving, i.e. the car was at x= Oat t=0 (Fig.
3.1).Let P, Qand R represent the positions of the car at different instants of
time. Consider two cases
ofmotion. In the first case, the car moves from Oto
P. Then the distance moved by the car is OP = +360 m. This distance is called
the path
length traversed by the car. In the second case, the
car moves from O to P and then moves back from P to Q. During this course of
motion,the path length traversed is OP + PQ = + 360m
+ (+120 m) = + 480 m. Path length is a scalar
quantity — a quantity that has a magnitude only and no direction (see Chapter
4).
Diaplacement
It is useful to define another quantity
displacement as the change in posttion. Let x, and
x, be the positions of an object at thne ¢,and f,. Then its displacement,
denoted by Ax, in
time At = {f, - t), is given by the difference
between the final and initial positions :
Ax= x,- x,
(We use the Greek letter delta (A) to denote a
change in a quantity.)
If x, > x, Axis positive; and if x, < x, Ax is
negative.
Displacement has both magnitude and
direction. Such quantities are represented by
vectors. You will read about vectors in the next chapter. Presently, we are
dealing with motion
along a straight line (also called rectilinear
motion) only. In one-dimensional motion, there are only two directions
(backward and forward,
upward and downward) in which an object can move,
and these two directions can easily be specified by + and - signs. For
example,displacement of the car in moving from © to P is:
Ax= x, -x, = (4360 m} -0 m= +360 m
The displacement has a magnitude of 360 m and is
directed in the positive x direction as indicated by the + sign. Similarly, the
displacement of the
car from P to G is 240 m - 360 m =- 120 m. The
negative sign indicates the direction of
displacement. Thus, it is not necessary to use
vector notation for discussing motion of objects in one-dimension.
The magnitode of displacement may or may
not be equal to the path length traversed by an
object. For example, for motion of the car from O to P, the path length is +360
m and the displacement is +360 m. In this case, the magnitude of displacement
(360 m) is equal to
the path length (360 m). But consider the motion of
the car from © to P and back to Q. In this case, the path length = (+360 m) +
(4120 m) = + 480 m. However, the displacement = (+240 m) -
(0 m) = + 240m. Thus, the magnitude of
displacement (240 m) is not equal to the path length
(480 m).
The magnitude of the displacement for a
course of motion may be zero but the
corresponding path Iength is not zero. For example,
if the car starts from O, goes to P and then returns to O, the final position
coincides with the initial position and the displacement
is zero. However, the path length of this journey is
OP + PO=360m+ 360m=720m.
Motion of an object can be represented by a
position-thime graph as you have already learnt about it. Such a graph is a
powerful tool to represent and analyse different aspects of motion of an
object. For motion along a straight
line, say X-axis, only x-coordinate varies with time
and we have an x-f graph. Let us first consider the simple case in which an object
is stationary, e.g. a car standing still at x= 40 m.
The position-time graph is a straight line parallel
to the time axis, as shown in Fig. 3.2(a).
If an object moving along the straight Hne covers
equal distances in equal intervals of time, it is said to be in mniform motion
along a straight line. Fig. 3.2(b) shows the position-time
graph of such a motion.
Now, let us consider the motion of a car that starts
from rest at time f= 0 8 from the origin O and picks up speed till f= 10 s and
thereafter moves with uniform speed till t= 18 s. Then the
Drakes are applied and the car stops at
t= 20 8 and x= 296 m. The position-time graph for
this case is shown in Fig. 3.3. We shall refer to this graph in our discussion
in the following sections.
3.3 AVERAGE VELOCITY AND AVERAGE
SPEED
When an object is in motion, its position changes
with time. But how fast is the position changing with time and in what
direction? To describe this, we define the quantity average welocity. Average
velocity is defined as the
change in position or displacement (Ax) divided by
the time intervals (A), in which the displacement occurs :
peter A 3.1)
ty-t, At
where x, and x, are the positions of the object at
time Land t,, respectively. Here the bar over the symbol for velocity is a
standard notation
used to indicate an average quantity. The SI unit
for velocity is m/s orm s", although om hr’ is used in many everyday
applications.
Like displacement, average velocity is also a vector
quantity. But as explained earlier, for motion in a straight line, the
directional aspect of the vector can be taken care of by + and -signs and we do
not have to use the vector notation for velocity in this chapter.
Consider the motion of the car in Fig. 3.3. The
portion of the x-t graph between f=0 s and t=8 9 is blown up and shown in Fig.
3.4. As seen from the plot, the average velocity of the car
between time t= 5s and {=7 sis:
- X%),-x, (27.4-10.0)m — ed
bm rasys Geometrically, this is the slope of the
straight line P,P, connecting the initial position P, to
the final posttion P, as shown in Fig. 3.4.
The average velocity can be posttive or negative
depending upon the sign of the displacement. It is zero if the displacement is
zero. Fig. 3.5 shows
the «-tgraphs for an object, moving with positive velocity
(Mig. 3.5a}, moving with negative velocity (Fig. 3.5b) and at rest (Fig. 3.5c).
Average velocity as defined above involves only the
displacement of the object. We have seen earlier that the magnitude of
displacement may
be different from the actual path length. To
describe the rate of motion over the actual path,we introduce another quantity
called average
speed.
Average speed is defined as the total path length
travelled dtvided by the total time interval during which the motion has taken
place :
Average speed = Total path length (3.2)
Total time inferval Average speed has obviously the
same unit (m s“) as that ofvelocity. But it does not tell us
in what direction an object is moving. Thus, it is
always positive (in contrast to the average velocity which can be positive or
negative). If the
motion of an object is along a straight line and in
the same direction, the magnitude of displacement is equal to the total path
length.In that case, the magnitude of average velocity Consider the motion of
the car in Fig. 3.3. The
portion of the x-t graph between f=0 s and t=8 9 is
blown up and shown in Fig. 3.4. As seen from the plot, the average velocity of
the car between time t= 5s and {=7 sis:- X%),-x, (27.4-10.0)m — ed
bm rasys
Geometrically, this is the slope of the straight
line P,P, connecting the initial position P, to the final posttion P, as shown
in Fig. 3.4.
The average velocity can be posttive or negative
depending upon the sign of the displacement. It is zero if the displacement is
zero. Fig. 3.5 shows
the «-tgraphs for an object, moving with positive
velocity (Mig. 3.5a}, moving with negative velocity (Fig. 3.5b) and at rest
(Fig. 3.5c).
Average velocity as defined above involves only the
displacement of the object. We have seen earlier that the magnitude of
displacement may
be different from the actual path length. To
describe the rate of motion over the actual path,we introduce another quantity
called average
speed.
Average speed is defined as the total path length
travelled dtvided by the total time interval during which the motion has taken
place :
Average speed = Total path length (3.2)
Total time inferval
Average speed has obviously the same unit (m s“) as
that ofvelocity. But it does not tell us in what direction an object is moving.
Thus, it is always positive (in contrast to the average
velocity which can be positive or negative). If the
motion of an object is along a straight line and in the same direction, the
magnitude of displacement is equal to the total path length.
In that case, the magnitude of average velocity is
equal to the average speed. This is not always the case, as you will sce in the
following example.Example 3.1 A car is moving along a straight line, say OP in
Fig. 3.1. It moves from O to Pin 18s and returns from PtoQ in 6.0 s. What are
the average velocity and average speed of the car in going (a)
from O to P ? and (b) from O to P and back toQ?
Answer (a)
: Displacement
Average velocity = ——_—_\_
Time interval
p-2360m _ + 20m s*
18s
‘ Path length
Average speed = ———_—_
Time interval
-360M _ 90 ms
18s
Thus, in thia case the average speed fs equal to the
magnitude of the average velocity.
(b) In this case,
: . Displacement +240 mn
Ave 2 velocity = = ——___
Pera COONS Fine interval (18+6.0) s
‘=+10 ms"
Average speed = _Path length_ = OP + PQ
Time interval At
© (3604120) m a
=————= 20ms
24s Thus, in this case the average speed is nat
equal to the magnitude of the average velocity. This happens because the motion
here involves change in direction so that the path length is
greater than the magnitude of displacement.This
shows that speed is, in general, greater than the magnitude of the velocity.
<If the car in Example 3.1 moves from O to P and comes back to O in the same
time interval,average speed is 20 m/s but the average velocity
is zero!
3.4 INSTANTANEOUS VELOCITY AND SPEED
The average velocity tells us how fast an object has
been moving over a given time interval but does not tell 1s how fast it moves
at different instants of time during that interval. For this,
we define instantaneous velocity or simply velocity
v at an instant ¢.
The velocity at an instant is defined as the limit
of the average velocity as the time interval Atbecomes infinitesimally small.
In other words,. ' ax
v= mm
4t30 Al 6.Sa)
ok (8.3b)
dt
where the symbol ane y Stands for the operation of
taking limit as ateo of the quantity on its right. In the language of calculus,
the quantity on the right hand side of Eq. (3.3a) ia the
differential coefficient of x with respect to tand
“as is denoted by — (see Appendix 3.1). It is the rate of change of position
with respect to time,
at that instant.
We can use Eq. (8.3a) for obtaining the vahie of
velocity at an inatant efther graphically or numerically. Suppose that we want
to obtain graphically the vane of velocity at time t=48 (point P} for the
motion of the car represented
in Fig. 3.3. The figure has been redrawn in Wig. 3.6 choosing different acales to facilitate
the calculation. Let us take At = 2 8
centred at t= 4s. Then, by the definition of the average velocity, the slope of
line P,P, { Fig. 3.6) gives
the value of average velocity over the interval 38
to5s. Now, we decrease the value of Af from 2atol1s. Then line P,P, becomes
O,Q, and its slope gives the vahic of the average velocity over
the interval 3.5 8 to 4.5 s. In the Hmit Af + 0,the
line P,P, becomes tangent to the position-time curve at the point P and the
velocity at t=43 is given by the slope of the tangent at that point. It is
difficult to show this process
graphically. But if we ase numerical method to
obtain the value of the velocity, the meaning of the limiting process becomes
clear. For the graph shown in Fig. 3.6, x= 0.08 & Table 3.1 gives the value
of Ax/At calculated for At equal to 2.0 s, 1.08, 0.5 8, 0.1 s and 0.01 5 centred
at t = 4.0 s. The
second and third columns give the value of f=t t
[: - at) and /. (e+) and the fourth and
the fifth cohmmns give the corresponding values of
x, i.e. x(f,) = 0.08 #? and x(t, = 0.08 73. The sixth column lists the
difference Ax = xt) -x (t) and the last column givea the ratio of Ax and
At, le. the average velocity corresponding to the value of Af listed in
the first column.
We see from Table 3.1 that as we decrease the value
of Af from 2.0 8 to 0.010 s, the vahie of the average velocity approaches the
limiting
value 3.84 m s? which is the vahue of velocity at
t=4.0 a, Le. the value of ~ at t= 4.0 s. In this manner, we can calculate
velocity at each instant for motion of the car shown in Fig. 3.3.
For this case, the variation of velocity with time
is found to be as shown in Fig. 3.7.
The graphical method for the determination of the
instantaneous velocity is always not a convenient method. For this, we must
carefully
plot the position-time graph and calculate the value
of average velocity as At becomes smaller and smaller. It is easier to
calculate the vahie
of velocity at different Instants if we have data of
positions at different instants or exact expression for the position as a
function of time.
Then, we calculate Ax/At from the data for decreasing
the value of At and find the limiting value as we have done in Table 3.1 or use
differential calculus for the given expression and dx
calculate UU at different instants as done in the
following example.
Example 3.2 The posttion of an object
moving along x-axts ts given by x=atbf
where a=85m,b=25ms7 andtis measured in seconds. What
ts tts veloctty at
t=Osandt=2.0 s. What ts the average
veloctty between t=2.0s andt=4.038?
Answer In notation of differential calculus, the
velocity is "dx od a. "1
ve e—f{asnt )=2bt=50tms dt dt At t=0a8, v=Oms"
andat t=2.08,v=10ms'.Average velocity = X(4.0)~ x(2.0) 4.0-2.0
_a+l6b-a-4b _ 6.0xb 2.0 =6.0%2.5=15ms" <
From Fig. 3.7, we note that during the period t=10 8
to 188 the velocity is constant. Between period t =18 s to t= 20 s, it ia
uniformly decreasing and during the perlodt=Osto t = 10s, it is increasing.
Note that for uniform
motion, velocity is the same as the average velocity
at all instants.
Instantancous speed or simply speed is the magnitude
of velocity. For example, a velocity of + 24.0 ms" and a velocity of -
24.0 m s'—both have an associated speed of 24.0 ms". It should be noted
that though average speed over a finite
interval of time is greater or equal to the
magnitude of the average velocity,
instantaneous speed at an instant is equal to the
magnitude of the instantaneous velocity
at that instant. Why so ?
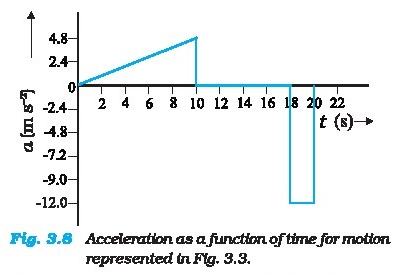
3.6 ACCELERATION
The velocity of an object, in general, changes
during its course of motion. How to describe this change? Should it be
described as the rate of change in velocity with distance or with time ?
This was a problem even in Galileo's time. It was
first thought that this change could be described by the rate of change of
velocity with distance.
But, through his studies of motion of freely falling
objects and motion of objecta on an inclined plane, Galileo concluded that the
rate of change
of velocity with time is a constant of motion for
all objects in free fall. On the other hand, the change in velocity with
distance is not constant — it decreases with the increasing distance of fall.
This led to the concept of acceleration as the rate
of change of velocity with time.
The average acceleration a over a time
interval is defined as the change of velocity
divided by the time interval :
a= by = BD, _ AU G- Al (3.4) where v, and v, are the
instantaneous velocities
or simply velocities at time ¢, and i, . It is the
average change of velocity per unit time. The SI unit of acceleration is ms? .
On a plot of velocity versus time, the average acceleration
is the slope of the straight line connecting the points corresponding to (u,,
§)and (v,, t,). The average acceleration for velocity-time graph shown in Fig.
3.7 for
different time intervals 0s - 108, 10s- 18s,and
18s-20sare:
= (24-0)ms" >qaic* s?Os-108 (10 -0)s 2.4ms
‘= (24-24)ms"! 5 qa A s?
108-188 (18-10)s Ooms = (0-24)ms" ~
- Q=————— = -12 ms*169-208 (20-18)s ms
Instantaneous acceleration is defined in the same way as the instantaneous velocity :
_ Av dv
a= ims di (3.5)The acceleration at an instant is the
slope of the tangent to the v-t curve at that instant. For
the v-t curve shown in Fig. 3.7, we can obtain
acceleration at every instant of time. The resulting a—t curve is shown in Fig.
3.8. We see that the acceleration is nonuniform over the
period 0 4 to 10 a. It is zero between 10 8 and 18 s
and is constant with value -12 m s* between 18 8 and 20 s. When the
acceleration is uniform, obviously, it equals the average acceleration over
that period.
Since velocity is a quantity having both
magnitude and direction, a change in velocity may
involve either or both of these factors.Acceleration, therefore, may result
from a change in speed (magnitude), a change in direction or changes in both.
Like velocity,
acceleration can also be positive, negative or zero.
Position-time graphs for motion with positive, negative and zero acceleration
are shown in Figs. 3.9 (a), {b) and (c), respectively.
Note that the graph curves upward for positive
acceleration; downward for negative acceleration and it is a straight line for
zero acceleration. As an exercise, identify in Fig. 3.3,
the regions of the curve that correspond to these
three casca.
Although acceleration can vary with time,our study
in this chapter will be restricted to motion with constant acceleration. In
this case,the average acceleration equals the constant
value of acceleration during the interval. If the
velocity of an object is vat t= 0 and vat time f,we have
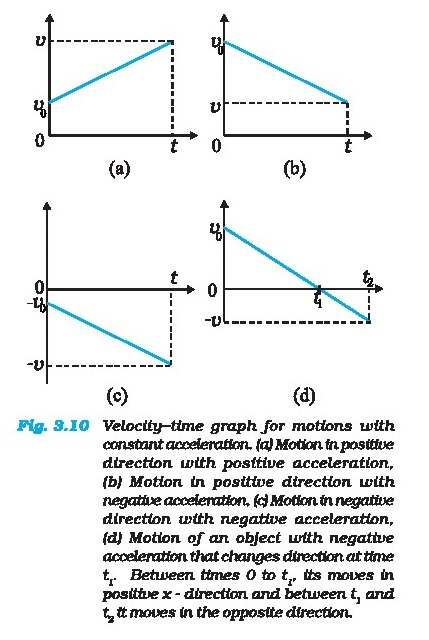
Let us see how velocity-time graph looks like for
some simple cases. Fig.3.10 shows velocity-time graph for motion with constant
acceleration for the following cases :
(a) Anobject is moving in a positive direction with
a positive acceleration, for example the motion of the car in Fig. 3.3 between
t=Osand t=10s8.,
(b) An object is moving in positive direction with a
negative acceleration, for example,motion of the car in Fig 3.3 between t=18s
and 20s.
(c) Anobject is moving in negative direction with a
negative acceleration, for example the motion of a car moving from O in Fig.3.1
in negative x-direction with increasing speed.
(d) An object is moving in positive direction till
time f,, and then turns back with the same negative acceleration, for example
the motion of a car from point O to point Q in Fig, 3.1 till time t, with
decreasing
speed and turning back and moving with
the same negative acceleration.
An interesting feature of a velocity-time graph for any moving object is that the area under the curve represents the displacement over a given time interval. A general proof
of this statement requires use of
calculus. We can,
however, see that it is true for the simple case of
an object moving with constant velocity u. Its velocity-time graph is as shown
in Fig. 3.11.The v-t curve isa straight line parallel to the
time axis and the area under it between t = 0 and t
= Tis the area of the rectangle of height u and base T. Therefore, area = u x
T= uT which
is the displacement in this time interval. How come
in this case an area is equal to a distance?
Think! Note the dimensions of quantities on the two
coordinate axes, and you will arrive at the answer.Note that the x-f, v-t, and
a-t graphs shown in several figures in this chapter have sharp
kinks at some pointe implying that the
fanctions are not differentiable at these points. In
any realistic situation, the functions will be differentiable at all pointe and
the graphs will be smooth.
What this means physically ie that
acceleration and velocity cannot change
values abruptly at an instant. Changes are always
continuous.
3.6 KINEMATIC EQUATIONS FOR
UNIFORMLY ACCELERATED MOTION
F
or uniformly accelerated motion, we can derive some simple equations that relate displacement(4, time taken (4, initial velocity (v,), final velocity (vj) and acceleration (aj. Equation (3.6)
already obtained gives a relation between final and
initial velocities vand v, ofan object moving with uniform acceleration a :
v=v,+at (3.6)This relation is graphically
represented in Fig. 3.12.
The area under this curve is :Area between instants
0 and ¢= Area of triangle ABC + Area of rectangle OACD
As explained in the previous section, the area under
v-t curve represents the displacement.Therefore, the displacement x of the
object is :x= Sev. )t+v,t (3.7)
But v=, = at Therefore, «= sa +t
. Ll or, Xx =Uytt+ at (3.3)Equation (3.7) can also
be written as x= oe =vt (3.9a)where,— vt Ug v= (constant acceleration
only)(3.9b)Equations (3.9a) and (3.9b) mean that the object
has undergone displacement x with an average
velocity equal to the arithmetic average of the initial and final velocities.From
Eq. (3.6), €=(v—v)/a. Substituting this in Eq. {3.9a), we get
on, (Vt Wvrw\ wu x=o1-[ 2 I a I- 2a
we v2 + 2ax (3.10)
This equation can also be obtained by
substituting the value of t from Eq. (3.6) into Eq.
(3.8). Thus, we have obtained three important equations :
v=v,+at
eet tat
X= Ugl + aa
‘ve? =e +2ax @.11a)
connecting five quantities v,, v, a, tand x. These
are kinematic equations of rectilinear motion for constant acceleration.
The set of Eq. (3.11a) were obtained by
asauming that at f = 0, the position of the
particle, xis 0. We can obtain a more general equation if we take the position
coordinate at t = 0 as non-zero, say x,. Then Eqs. @.11a) are
modified (replacing x by x—x, ) to:
v=v, + at X= Xp t+ vot + Sar" (3.11b)
‘ws ug + 2alx — x,y) .11¢)Exampte 3.3 Obtain
equations of motion for constant acceleration using method of calculus.
Answer By definition | _ dv dt
dv=adt Integrating both sides J . de = fia dt =al .
dt (ais constant)‘v-v, sat ‘vs Vy tat Further, v= dx dt dx=vdt
Integrating both sides J : dx = fie dt
=f ile +at) dt
xox =y, tela
oh 2
: ls
X =Xt t+5at
We can write
qa dv_dv dx _, dv
di dx dé = dx
or, udu=adx
Integrating both sides,
J. ude = jc adx
as = a{x-x,}
vw? su! +2a(x - x.)
The aclvantage of this method ts that it can be used
for motion with non-uniform acceleration also.
Now, we shall use these equations to some important
casea. <Example 3.4 A ball is thrown vertically upwards with a velocity of
20 m s? from the top of a multistorey building. The height of the point from
where the ball ts thrown is 25.0 m from the ground. (a) How
high will the ball rise ? and (b) how long will it
be before the ball hits the ground?
Take g=10ms"%.
Answer (a} Let us take the y-axis in the
vertically upward direction with zero at the ground,
as shown in Fig. 3.13.
Now v,=+20ms",
a=-g=-l0ms"’,
v=Oms'
If the ball rises to height y from the point of
launch, then using the equation
v= v2 +2a (y-y)
we get
O = (20)? + 2C-10)[y — y,)
Solving, we get, (y-y,) = 20 m.
(b) We can solve this part of the problem in two
ways. Note carefully the methods used.
FIRST METHOD : In the first method, we split the
path in two parts : the upward motion (A to B) and the downward motion (B to C)
and calculate the corresponding time taken f, and &. Since the velocity at
B is zero, we have :
v= v,+ at
0=20 -106,
Or, t=28
This is the time in going from Ato B. From B, or the
point of the maximum height, the ball falls freely under the acceleration due
to gravity. The
ball is moving in negative y direction. We use
equation
U= Yo + vot +5at*
We have, y, = 45m, y=0, v,=0, a=—g =-lOms*
O = 45 + (4) 10) f?
Solving, we get t, = 3s
Therefore, the total time taken by the ball before
ft hits the ground =f, + §, = 28+3s8=5a.,SECOND METHOD : The total time taken
can also be calculated by noting the coordinates of initial and final positions
of the ball with respect
to the origin chosen and using equation
1 2
Y=Uat Bol + gar
Now y, = 25m y=Om
v,=20m s", a =-10ms*, t=?
O=25 +20 +(%) 10) 2
Or, 5@-20t -25 =0
Solving this quadratic equation for f, we get t=5s
Note that the second method is better since we do not have to worry about the
path of the motion
aa the motion is wnder constant acceleration.Example
3.6 Free-fall : Discuss the motion of an object under free fall. Neglect air
resistance.
Answer An object released near the surface of the
Earth is accelerated downward under the influence of the force of gravity. The
magnitude
of acceleration due to gravity is represented by g.
If air resistance ts neglected, the object is said to be in free fall. If the
height through
which the object falls is small compared to the '
‘earth's radius, g can be taken to be constant,equalto 9.8 ms“. Free fall is
thus a case of motion with untform acceleration.
: We assume that the motion is in y-direction,more
correctly in -y-direction because we choose upward direction aa positive. Since
the acceleration due to gravity is always downward,it is in the negative
direction and we have
a=-g =-9.8ms*
‘The object is released from rest at y=0. Therefore,' _¥, = O and the equations of motion become:
v= 0-gt =-908t ms
y= 0-% gf =490 m
w=0-2gy =-19.6y m'*s*
These equations give the velocity and the distance
travelled as a function of time and also the variation of velocity with
distance. The variation of acceleration, velocity, and distance,
‘With time have been plotted in Fig. 3.14{a), (b)and
(c).
Fig. 3.14 Motton of an object under free fall.
(a) Variation of acceleration with time,
(b) Variation of veloctty with time.
(c} Variation of distance with time <
Example 3.6 Galileo's law of odd
numbers: “The distances traversed, during equal
intervals oftime, by a body falling Jrom rest, stand to one another in the same
ratio as the odd numbers beginning with untty [pamely, 1:3: 5: 7......].° Prove
it,Answer Let us divide the time interval of motion of an object under free
fall into many equal intervals t and find out the distances
traversed during successive intervals of
time. Since initial velocity is zero, we have 1 I y
2 gt Using this equation, we can calculate the position of the object after
different time intervals, 0, €, 2t, 31... which are given in second column of
Table 3.2. If we take
(1/2) gt*as y,—the position coordinate after first
time interval 7, then third column gives the positions in the unit of y,. The
fourth column gives the distances traversed in successive ts. We find that the
distances are in the simple ratio 1: 3; 5: 7:9; 11...as shown in the last
column. This law was established by Galileo Galilei (1564-1642) who was the firat
to make quantitative studies of free fall. <
Example 3.7 Stopping distance of
vehicles : When brakes are applied to a
moving vehicle, the distance it travels before
stopping is called stopping diatance. It is an important factor for road safety
and depends on the initial velocity (u,) and the braking capactty, or
deceleration, -a that is caused by the braking. Derive an expression for
stopping distance ofa vehicle
in terma of v, anda.
Answer Let the distance
travelled by the vehicle
before it stopa be d,. Then, using equation of
motion i =y,7 +2 ax, and noting that v=0, we have the stopping distance = 05 d.
= 2a Thus, the atopping distance is proportional to the square of the initial
velocity. Doubling the
initial velocity increases the stopping distance by
a factor of 4 (for the same deceleration).For the car ofa particular make, the
braking distance was found to be 10 m, 20 m, 34m and 50 m corresponding to
velocities of 11, 15, 20 and 25 m/s which are nearly consistent with the above
formula.
Stopping distance is an important factor
considered in setting speed limits, for example,in
school zones. <
Example 3.8 Reaction time: When a situation demands our immediate
action, it takes some time before we really respond. Reaction time is the
time a person takes to observe, think and act. For example, if a person is
driving and suddenly a boy appears on the road, then the time elapsed before
he slams the brakes of the car is the reaction time. Reaction time depends
on complexity of the situation and on an individual.
You can measure your reaction time by a simple experiment. Take a ruler
and ask your friend to drop it vertically through the gap between your thumb and forefinger (Fig. 3.15). After you catch it, find the distance d travelled by the ruler. In a particular case, d was found to be 21.0 cm. Estimate reaction time.
"al :
Friese han
Ruler
an = ve "
i a
Fig. 3.15 Measuring the reaction time.
Answer The ruler drops under free fall.
Therefore, uv, = 0, and a =-g=-9.8 m s*. The
distance travelled d and the reaction time ¢, are related by
: 1,
d= 7) GF
oO, f= (2 8
Given d = 21.0 cm and g=9.8m s*the reaction
time is
t,= oH s=O0.2s. <
3.7 RELATIVE VELOCITY
You must be familiar with the experience of
travelling in a train and being overtaken by another train moving in the same
direction as you are. While that train must be travelling faster
than you to be able to pass you, ft does seem slower
to you than it would be to someone standing on the ground and watching both the
trains. In case both the trains have the same velocity with respect to the
ground, then to you
the other train would seem to be not moving at all.
To understand such observations, we now introduce the concept of relative
velocity.
Consider two objects A and B moving
uniformly with average velocitica v, and v, in one
dimension, say along x-axis. (Unless otherwise specified, the velocities
mentioned in this chapter are measured with reference to the
ground). If, (0) and x, (0) are positions of objects
Aand B, reapectively at time t= 0, their positions
x, (9 and x, (§ at time t are given by:
x, (6) = x,O) +, t {3.12a)
xX, (6 = x, ©) + vt (3.12b)
Then, the displacement from object A to object Bis
given by
x, f{8 = x, - x, @
= [x, (0) - x, (0) ] + (u,-0) & (3.13)
Equation (3.13) is easily interpreted. It tella us
that as seen from object A, object B has a velocity v,—v, because the
displacement from Ato Bchanges steadily by the amount v,— v, in
each unit of time. We say that the velocity of
object B relative to object A is v,—vu,:Va, = U5 — Vy (3.14a)
Similarly, velocity of object A relattue to object B
fs:v5 = 0,-4, (3.14b)
This shows: Van = — Uy (3.14)
Now we consider some special cases :
(a) Ifo, =v,, u,-v, =O. Then, from Eq. (3.13), x,
(6 - x, (§ = x, (0) - x, (0). Therefore, the two
objects stay at a constant distance (x, (0) - x,
(0)) apart, and their position-time graphs are
straight lines parallel to each other as shown in Fig. 3.16. The relative
velocity v,, or v,, 1s
zero in this case.
(b) If v, > v,, v, — v, is negative. One graph is
steeper than the other and they meet at a common point. For exampk, suppose v,
=20ms" and x, (0) = 10 m; and vu, = 10 ms", x, (0} = 40 m; then the
time at which they meet is t= 3s
(Fig. 3.17). At this instant they are both at a
position x, (@ = x, (0 = 70 m. Thus, object A overtakes object B at this time.
In this case,v,,=10me'-20me' =-l10ms"=- up,
(c) Suppose yu, and u, are of opposite signs. For
example, if in the above example object A is moving with 20 ms“ starting at
x,(0} = 10m and object B is moving with - 10 ms“ starting
at x, 0) = 40m, the two objecta meet at t= 1 5 (Fig.
3.18). The velocity of B relative to A,Uy = I-10 -(20)] m s* =-30 m s'=—»,,..
In this case, the magnitude of v,, or v,, {= 30 m a") is greater than the
magnitude of velocity of A or
that of B, Ifthe objects under consideration are two
trains, then for a person sitting on either of the two, the other train seems
to go very fast.
Note that Eq. (3.14) are valid even if v, and
u,represent instantaneous velocities.
Example 3.9 Two parallel rail tracks run
north-south. Train A moves north with a
speed of 54 lon Ir’, and train B moves south with a
speed of 90 Ion hr’. What is the
(a) veloctty of B with respect to A?,
(b) velocity of ground with respect to B?,and
(c) velocity of a monkey running on the
roof of the train A against fts motion
(with a velocity of 18 km bh’ with
respect to the train A) as observed by
aman standing on the ground ?
Answer Choose the positive direction of x-axis to be
from south to north. Then,
v,2 +54kmh? = 15ms!
v, = -90 kmh’ = -25ms!
Relative velocity of B with respect to A= v,,—
v,=-40ms' , i.e. the train B appears to A to move with a speed of 40 m s” from
north to south.Relative velocity of ground with respect to
B=0-v,=25ms".
In (Cc), let the velocity of the monkey with respect
to ground be u,,. Relative velocity of the mankey with respect to A,v=
u,—0,=-18 km hr’ =-5 ms". Therefore,uv, =(15-5)ms'=10ms".
SUMMARY
1. An abject is said to be in motion if its poaition
changes with time. The position of the object can be specified with reference
to a conveniently chosen origin. For motion in a straight line, position to the
right of the origin is taken as positive and to the left as
negative.
2. Path tength is defined as the total length of the
path traversed by an object.
3. Displacementis the change in position: Ax =
x,-—x,. Path length is greater or equal to the magnitude of the displacement
between the same points.
4. An object is said to be in uniform motion in a
straight line if its displacement is equal in equal intervals of time.
Otherwise, the motion is said to be non-uniform
5. Average veloctty is the displacement divided by
the time interval in which the displacement occurs :
— Ax
v=—
At
On an «xt graph, the average velocity over a time
interval is the slope of the line connecting the initial and final posttions
corresponding to that interval.
6. Average Speed is the ratio of total path length
traversed and the corresponding time interval.The average speed of an object is
greater or equal to the magnitude of the average velocity over a given time
interval.
7. dJnstantaneous velocity or simply velocity is
defined as the limit of the average velocity as the time interval At becomes
infinitesimally amall :
oy AK dx
v= lim v= im — =—
Atou atau At dt
The velocity at a particular instant is equal to the
alope of the tangent drawn on position-time graph at that instant.
8. Average acceleration ia the change in velocity
divided by the time interval during which the change occurs :
quate oN
9. Instantaneous acceleration is defined as the
limit of the average acceleration as the time interval At goes to zero :
a- lima= lim Av _ de
Afou Abou At ~ dt
The acceleration of an object at a particular time
is the slope of the velocity-time graph at that instant of time. For uniform
motion, acceleration is zero and the xt graph is a straight line inclined to
the time axis and the ut graph is a straight ine
parallel to the time axis. For motion with uniform
acceleration, xt graph is a parabola while the v-t graph is a straight line
inclined to the time axis.
10, The area under the velocity-time curve between
times f, and £, is equal to the displacement of the object during that interval
of time.
11, For objects in uniformly accelerated rectilinear
motion, the five quantities, displacement x, time taken ¢, initial velocity v,,
final velocity v and acceleration a are related by a set
of simple equations called kinematic equations of
mation :
v=u,+ at
: Io,
X= vyol+—at™
2
v? = vs + 2ax
if the position of the object at time t= 0 fa 0. If
the particle starts at x =x, , xin above equations ta replaced by (x - x,).
MOTION IN A STRAIGHT LINE 65
Cee POINTS TO PONDER
1. The path length traversed by an object between
two points ia, in general, not the eame as the magnitude of displacement. The
displacement depends only on the end pointe:
the path length (as the name implies} depends on the
actual path. In one dimension,the two quantities are equal only if the object
does net change its direction during the course of motion. In all other cases,
the path length is greater than the magnitude of
displacement.
2. In view of point 1 above, the average speed of an
object ie greater than or equal to the magnitude of the average velocity over a
given time interval. The two are equal only if the path length is equal to the
magnitude of displacement.
3. The origin and the poaitive direction of an axis
are a matter of choice. You should first specify this chaice before you assign
signs te quantities like displacement, velocity and acceleration.
4 Ifa particle is speeding up, acceleration is in
the direction of velocity; if ite speed ie decreasing, acceleration is in the
direction opposite to that of the velocity. Thies
statement is independent of the choice of the origin
and the axis.
5. The align of acceleration does not tell us
whether the particle's speed is increasing or decreasing. The sign of
acceleration (as mentioned in point 3) depends on the choice of the positive
direction of the axis. For example, if the vertically upward direction ie
chosen to be the positive direction of the axis, the
acceleration due to gravity is negative. If a particle is falling under
gravity, this acceleration, though
negative,
resulte in increase in epeed. For a particle thrown
upward, the same negative acceleration (of gravity) results in decrease in
speed.
6. The zero velocity of a particle at any instant
does not necessarily imply zero accelcration at that instant. A particle may be
momentarily at rest and yet have non-zero acceleration. For example, a particle
thrown up has zero velocity at ite uppermost point but the acceleration at that
instant continues to be the acceleration due to gravity.
7. In the kinematic equations of motion [Eq.
(3.11)]. the various quantities are algebraic,i.e. they may be positive or
negative. The equations are applicable in all situations (or one dimensional
motion with constant acceleration) provided the values of different
quantities are substituted in the equations with
proper signs.
8. The definitions of instantancous velocity and
acceleration (Eqs. (3.3) and (8.5)) are exact and are always correct while the
kinematic equations (Eq. (3.11)) are true only for motion in which the
magnitude and the direction of acceleration are constant during the course of
motion.
EXERCISES
3.1 In which of the following examples
of motion. can the body be considered approximately a point object:
(a) a railway carriage moving without jerks between
two stations.
(b) a monkey sitting on top of a man cycling
smoothly on a circular track.
(c) a spinning cricket ball that turns sharply on
hitting the ground.
(d) a tumbling beaker that has slipped off the edge
of a table.
3.2 The posttion-time (x- graphs for two children A
and B returning from their school O to their homes P and Q respectively are
shown in Fig. 3.19. Choose the correct entries in the brackets below ;
(a) (A/B) lives closer to the school than (B/A)
(b) (A/B) etarte from the school earlier than (B/A)
(c) (A/B) walke faster than (B/A)
(d) A and B reach homie at the (same/different) time
(e) (A/B) overtakes (B/A) on the road (once/twice).
3.3 A woman starts from her home at 9.00 am, walke
with a speed of 5 km h7! ona
straight road up to her office 2.5 km away, stays at
the office up to 5.00 pm, and returns home by an aute with a speed of 25 km
h-!, Choose suitable ecalea and
plot the x-t graph of her motion.
3.4 A drunkard walking in a narrow lanc takes 5
steps forward and 3 steps backward,followed again by 5 steps forward and 3
eteps backward, and se on. Each step is 1 mm long and requires 1 s. Plot the
x-t graph of his motion. Determine graphically and otherwise how long the
drunkard takes to fall in a pit 13 m away from the start.
3.5 A jet aizplane travelling at the speed of 500 km
h7! ejects its products of combustion at the speed of 1500 lan h-! relative to
the jet plane. What is the speed of the latter with reepect to an observer on
the ground ?
3.6 Acar moving along a straight highway with speed
of 126 km h~! is brought to a
stop within a distance of 200 m. What is the
retardation of the car {assumed
uniform), and how long does it take for the car to
stop 7
3.7 ‘Two trains A and B of length 400 m each are
moving on two parallel tracks with a uniform epeed of 72 km h7! in the same
direction, with A ahead of B. The driver of B decides to overtake A and
accelerates by 1m s%. Ifafter 50 s, the guard of B just brushes past the driver
of A, what was the original distance between them ?
3.8 On a two-lane road, car A is travelling with a
speed of 36 km h-!, Two care B and C approach car A in opposite directions with
a speed of 54 km h-! each. Ata certain instant, when the distance AB is equal
to AC, both being 1 Ian, B decides to overtake A before C does. What minimum
acceleration of car B ia required to avoid an accident ?
3.9 Two towns A and B are connected by a regular bus
service with a bus leaving in elther direction every T minutes. A man cycling
with a speed of 20 km h7! in the direction A to B notices that a bus goes past
him every 16 min in the direction of his motion, and every 6 min in the
oppoatte direction. What is the period T of the bus service and with what speed
(assumed constant) do the buses ply on the road?
3.10 Aplayer throws a ball upwards with an initial
speed of 29.4 m s*.
(a) What is the direction of acceleration during the upward motion of the
ball ?
(b) What are the velocity and acceleration of the
ball at the highest point of its motion ?
(c) Choose the x = 0 m and t = 0 a to be the
location and time of the ball at ita
highest point, vertically downward direction to be
the positive direction of x-axis, and give the signs of position, velocity and
acceleration of the ball during its upward, and downward motion.
(a) To what height does the ball rise and after how
long does the ball return to the player's hands ? (Take g = 9.8 m s* and
neglect air resistance).
3.11 Read each statement below
carefully and state with reasons and examples, if it is true or false ;
Aparticie in one-dimensional motion
(a) with zero speed at an instant may have non-zero
acceleration at that instant
(b) with zero speed may have non-zero velocity,
(Q) with constant speed must have zero acceleration,
(d) with positive value of acceleration must be
speeding up.
3.12 Aball is dropped from a height of 90 m on a
floor. At each collision with the floor,the ball loses one tenth of ite speed.
Plot the speed-time graph of ite motion between t= 0 to 12 a.
3.13 Explain clearly, with examples, the distinction
between :
(a) magnitude of displacement (sometimes called
distance) over an interval of time,and the total length of path covered by a
particle over the same interval;
(b) magnitude of average velocity over an interval
of time, and the average speed over the eame interval. [Average speed of a
particle over an interval of time is defined as the total path length divided
by the time interval]. Show in both (a)and (b) that the second quantity is
either greater than or equal to the first.When is the equality sign true ? [For
simplicity, consider one-dimenaional motion only].
3.14 Aman walks on a straight road from hie home to
a market 2.5 kan away with a
speed of 5 km h-!, Finding the market closed, he
instantly tums and walks back
home with a speed of 7.5 km h7!, what is the
(a) magnitude of average velocity, and
(b) average speed of the man over the interval of
time i) 0 to 30 min, (ti) 0 to 50 min, [fit] 0 to 40 min ? [Note: You will
appreciate from this exercise why it is better to define average speed as total
path length divided by time, and not ae magnitude of average velocity. You
would not like to tell the tired man on his return home that hie average speed
was zero !]
3.15 In Exercises 3.13 and 3.14, we have carefully
distinguished between average speed and magnitude of average velocity. No such
distinction is necessary when we
consider instantaneous speed and magnitude of
velocity. The inatantancous speed is always equal to the magnitude of
instantaneous velocity. Why ?
3.16 Look at the graphs (a) to (d) (Fig. 3.20)
carefully and state, with reasons, which of these cannot posaibly represent
one-dimensional motion of a particle.
3.17 Figure 3.21 shows the vc-t plot of one-dimensic
motion of a particle. Is it correct to say from -graph that the particle moves
in a straight line
t<0 and on a parabolic path for t >0 ? If not,
sugg a suitable physical context for this graph.
3.18 A police van moving on a highway with a speed
30 kan h* fires a bullet at a thiefs car speeding av in the same direction with
a speed of 192 km bh"
the muzzle speed of the bullet ts 150 m s°, v what
speed does the bullet hit the thiefs car ? (Nc Obtain that speed which ie
relevant for damag the thiefs car).
3.19 Suggest a suitable physical situation for each of:folowing graphs (Fig 3.22):
3.20 Figure 3.23 gives the x-t plot of a particle
harmonic motion. (You will learn about thie mot
Give the signa of position, velocity and acceler:
€=0.36,1.28,-12a
3.21 Figure 3.24 gives the x-it plot of a particle
in one-dimensional motion.
Three different equal intervals of time
are shown. In which interval ia the
average speed greatest, and in which
ia it the least ? Give the aign of average velocity
for each interval.
3.22 Figure 3.25 gives a speed-time graph of a
particle in motion along a constant direction. Three equal intervals of time
are shown. In which interval ie the average acceleration greatest in magnitude
? In which interval ia the average speed greatest ? Choosing the positive
direction as the constant direction of motion, give the signe of v and a in the
three intervals. What are the accelerations at the points A, B, C and D?
Additional Exercises
3.23 A three-wheeler starts from rest, accelerates
uniformly with 1 m s* on a straight road for 10 s, and then moves with uniform
velocity. Plot the distance covered by the velhidle during the n™ second fn = 1.2,3....)
versus n. What do you expect this plot to be during accelerated motion : a
straight line or a parabola ?
3.24 A boy standing on a stationary lift (open from
above) throws a ball upwards with the maximum initial speed he can, equal to 49
m =. How much time does the ball take to return to hia hands? If the lift
starta moving up with a uniform speed of 5 me" and the boy again throws
the ball up with the maximum apeed he can, how long does the ball take to
return to his hands ?
3.25 On a long horizontally moving belt (Fig. 3.26),
a child runs to and fro with a speed 8kmh ' (with respect to the belt} between
his father and mother located 50 m apart on the moving belt. The belt moves
with a speed of 4 km bh". For an obecrver on a stationary platform outalde,
what is the
(a) speed of the child running in the direction of
motion of the belt ?.
(b) speed of the child running opposite to the
direction of motion of the belt ?
(c) time taken by the child in (a) and (b) ?Which of
the answers alter if motion is viewed by one of the parents ?
3.26 Two stones are thrown up simultaneously from
the edge of a cliff 200 m high with initial speeds of 15 m s* and 30 m s*.
Verify that the graph shown in Fig. 3.27 correctly represents the time
variation of the relative position of the second stone with respect to the
first. Neglect air resistance and assume that the stones do not rebound after
hitting the ground. Take g = 10 m s*. Give the equations for the Hnear and
curved parts of the plot.
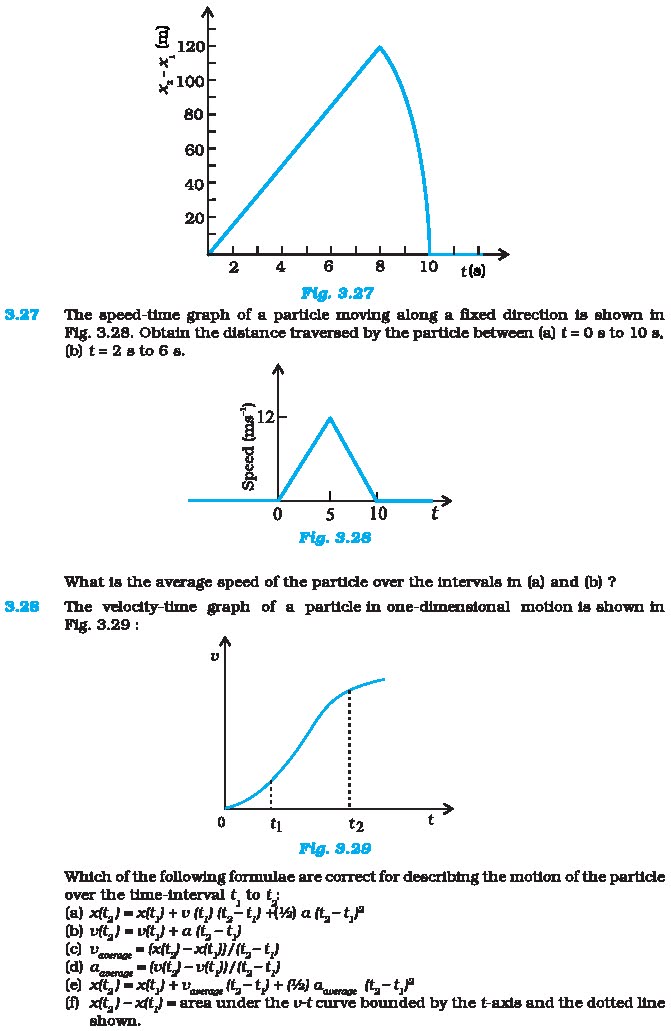
3.27 The speed-time graph of a particle movin ig
along a fixed direction is shown in Fig. 3.28. Obtain the distance traversed by
the particle between (a) t = 0 » to 10 a,(b) t= 2 ato6s,
What is the average speed of the particle over the
intervals tn (a) and (b) ?
3.28 The velocity-time graph of a particle in
one-dimensional motion ts shown in Fig. 3.29 :Which of the following formulae
are correct for deecribing the motion of the particle
over the time-interval ¢ to E:
(a) aft, = xity + v tty ft, ty 9) aft, t
(b) vft,) = vit} + a fi,-t)
(0) cserage @ Exley — tt, B/fE,— E)
(2) rage = ti) — VEE HI tit)
() EG) = EE) + Varerage fg— te) + PA) Oarerage ,-¢F7
(49) xft,) — 24} = area under the v-¢ curve bounded by the t-axis and the
dotted line ehown.
APPENDIX 3.1; ELEMENTS OF CALCULUS
Differential Calculus Using the concept of
‘differential coefiicient’ or ‘derivative’, we can easily define velocity and
acceleration. Though you will learn in detail in mathematics about derivatives,
we shall introduce
this concept in briefin this Appendix so as to
facilitate its use in describing physical quantities involved in motion.
Suppose we have a quantity y whose value depends
upon a single variable x, and is expressed by an equation defining y as some
specific function of x. This is represented as:y=fa (1)
This relationship can be visualised by drawing a
graph of function y = fd regarding y and xas Cartesian coordinates, as shown in
Fig. 3.30 (a).
Consider the point P on the curve y = f(x) whose
coordinates are (x, y) and another point 9 where coordinates are (x + Ax, y +
Ay). The slope of the line joining P and Q is given by:, _ ay y+ Ay -V tang =
AL = Weay-y (2)Suppose now that the point Q moves along the curve towards P. In
this proceas, Ay and Ax
decrease and approach zero; though their ratio »
will not necesaartly vanish. What happens A to the line PQ as Ay 0, Ax 0. You
can see that this line becomes a tangent to the curve at point P as shown in
Fig. 3.30{b). This means that tan @ approaches the slope of the tangent at P,
denoted by m:
a Ay (y+ ayy me fa Nae )The lrdt of the ratio Ay/Ax
as Ax approaches zero is called the derivative of y with respect to x and is
written as dy/dx. It represents the slope of the tangent line to the curve y =
f(x) at the
point (&, y).Since y = f(¥ and y + Ay = f(x +
AX, we can write the definition of the derivative aa:‘dy _df)_ ay, [fet An -
foo ‘dx dx = jy $2 Ax Given below are some elementary formulae for derivatives
of functions. In these u (xj and v(x)
represent arbitrary functions of x, and a and b
denote constant quantities that are independent of x. Derivatives of some
common functions are also listed .
62 PHYSICS
dau) _ du , dul de &
dx dx "dt dx de
‘d(u/e 1d dv
deur) _ dv, de ; ause) _ 1 du _ de
dx dx dx dx uw dx dx
du _ du/dx
dv dv/dx
4 Gin x)=cosx : a (cosx) = - sinx
ax . dx d
4 tan x) = sec? x ; 4 eotay= cos ec xX
dx =s H Tx Ota) = —Cos ec” x
d “d 2
— (see x)=tanx secx : — (cosec*x] =-cot x cosec x
dx dx
a rt no] ue . a ai
at anu aS ; de dn uw 7
4 ay gt
au Jee
In terms of derivatives, instantaneous velocity and
acceleration are defined as
t= It A dk t = ab At de _. Av dv dx
a=lin —=—=—Au At dt) dt Integral Calculus You are
familiar with the notion of area. The formulae for areas of simple geometrical
figures are
also known to you. For example, the area of a rectangle
is length times breadth and that of a triangle is half of the product of base
and height. But how to deal with the problem of determination
of area of an irregular figure? The mathematical
notion of integral is necessary in connection with
such problems.
Let us take a concrete example. Suppose a variable
force f(x) acts on a particle in its motion along x-axis from x=atox=b. The
problem is to determine the work done (W) by the force on the
particle during the motion. This problem is
discussed in detail in Chapter 6.
Figure 3.31 shows the variation of F(x) with x.
Ifthe force were constant, work would be simply the area F'(b-a) as shown in
Fig. 3.31(. But in the general case, force is varying .
F
I I
Xe ' '
0 a b 0 x XM eX
@ Gii)
Fig. 3.31
To calculate the area under this curve [Fig. 3.31
[if], let us employ the following trick. Divide the
interval on x-axis from a fo b into a large number
(N) of small intervals: x,[=a) to x,, x, to xg Xz f0 Xq,
sscecceececcessetsarsessessceece Miy_p UO Xz (=5). The
area under the curve is thus divided into N strips. Each atrip
is approximately a rectangle, since the variation of
Ft) over a strip is negligible. The area of the {
strip shown [Fig. 3.31(if] is then approximately
‘AA = F(x); - <j2)) = F(x, Jax
where Ax is the width of the strip which we have
taken to be the same for all the strips. You may wonder whether we should put
FUx,;) or the mean of Fxg and Ftx,,) in the above expression. If we
take Nto be very very large (N-9e), it does not
really matter, since then the strip will be so thin that the difference between
F(x) and F{x,,) is vanishingly small. The total area under the curve then is:‘
N N As ya = > Fevax
isl i=l
The limit of this suum as N-e- is known as the
integral of Fi) over x from a to b. It is given.a special symbol as shown
below:‘ b As [Fax
The integral sign | looks Hike an elongated S,
reminding us that it basically is the limit of the sum
of an infinite number of terms.
Amost significant mathematical fact is that
integration is, in a sense, an inverse of differentiation.Suppose we have a
function g (x) whose derivative is f(x), i.e. flo = 2
The function g (< fs known as the indefintte
integral of f(9 and is denoted as:gx) =| floax
An integral with lower and upper limita is known as
a definite integral. It ia a mumber. Indefinite integral haa no limits; it is a
function.
A fundamental theorem of mathematics statea that 'b
fseade= gol, = gb)- fa)
As an example, suppose f(xj =.¢ and we wish to
determine the value of the definite integral from x=l tox=2. The function g (x)
whose derivative is x“ia °/3. Therefore,‘2 ap .
4 x 8 1 _7
Joans| =3-3°F
1 1
Clearly, to evalnate definite integrals, we need to
know the corresponding tndefinite integrals. Some common indefinite integrals
are
. wit]
fxtdx = ~— (n #-1)
ntl
‘tl
Jax = Inx (x > 0)
x
Joinx dx = -cosx Jeosx dx = sinx
Jetdx=e*
This introduction to differential and integral
calculus ts not rigorous and is intended to convey to you the basic notions of
calculus.