Chapter 10 Mechanical Properties Of Fluids

CHAPTER NO.10 MECHANICAL PROPERTIES OF FLUIDS

 

10.1 INTRODUCTION

In this chapter, we shall study some common physical properties of Wqutis and gases. Liquids and gases can flow

and are therefore, called fluids. It is this property that datinguishes Hquids and gases from solids in a hasic way.

 

Fluids are everywhere around us. Earth has an envelop of air and two-thirds of fis surface is covered with water. Water

1a not only necessary for our existence; every mammalian body constitute mostly of water. All the processes occurring

in living beings including plants are mediated by fluids. Thus understanding the behaviour and properties of fluids is important.

 

How are fluids different from solids? What is common in Hguids and gases? Unlike a solid, a fluid has no definite

shape of its own. Soltds and liquids have a fixed volume,whereas a gas fills the entire volume of its container. We

have learnt in the previous chapter that the volume of solids can be changed by stress. The volume of solid, Bquid or gas depends on the stress or pressure acting on it. When we talk about fixed volume of solid or liquid, we mean its volume under atmospheric pressure. The difference between gases and solids or liquids is that for solids or liquids the change in volume due to change of external pressure is rather amall.

In other words solids and liquids have much lower compressibility as compared to gases.

 

Shear stress can change the shape of a solid keeping its volume fixed. The key property of flutds {s that they offer

very little resistance to shear stress; their shape changes by application of very small shear stress. The shearing stress of fluids is about million times smaller than that of solids.

 

102 PRESSURE

Asharp needle when pressed against our skin pierces it. Our skin, however, remains totact when a blunt object with a wider contact area (say the back of a spoon) is pressed against it with the same force. If an elephant were to step on a man's cheat, his ribs would crack. Acircus performer across whose chest a large, light but strong wooden plank is

Placed first, is saved fram this accident. Such everyday experiences convince us that both the force and its coverage area are important. Smaller

the area on which the force acts, greater is the impact. This concept is known as pressure.

 

When an object is submerged in a fluid at rest, the fluid exerts a force on its surface. This force is always normal to the object’s surface.This is so because if there were a component of force parallel to the surface, the object will also exert a force on the fluid parallel to it; as a consequence of Newton's third law. This force ‘will cause the fluid to flow paralle] to the surface.

Since the fluid is at rest, this cannot happen.Hence, the force exerted by the fluid at rest has to be perpendicular to the surface in contact with it. This is shown in Fig.10.1 (a).

 

The nonnal force exerted by the fluid at a point may be measured. An idealised form of one such pressure-measuring device is shown in Fig.10.1(b). It consists of an evacuated chamber with

a spring that is calibrated to measure the force acting on the piston. This device is placed at a point inside the fluid. The inward force exerted

by the fluid on the piston is balanced by the outward spring force and is thereby measured.

If Fis the magnitude of this normal force on the piston of area A then the average pressure P,,is defined as the normal force acting per unit area.

F

Pav =F (10.1)

 

In principle, the piston area can be made arbitrarily small. The pressure is then defined in a limiting sense as

“tim AF

P=.) a (10.2)

 

Pressure is a scalar quantity, We remind the reader that it is the component of the force normal to the area under consideration and not the (vector) force that appears in the numerator in Eqs. (10.1) and (10.2). Its dimensions are

[ML"T*]. The SI unit of pressure is Nm”. It has been named as pascal (Pa) in honour of the French scientist Blaise Pascal (1623-1662) who carried out pioneering studies on fluid pressure.

A common unit of pressure is the atmosphere (atm), i.e. the pressure exerted by the atmosphere at sea level (1 atm = 1.013 x 10° Pa).

 

Another quantity, that is indispensable in describing fhiids, is the density p. For a fluid of mass m occupying vohume V,p= (10.3)

 

The dimensions of density are [ML“]. Its SI unit is kg m™. It is a positive acalar quantity. A liquid is largely incompressible and its density

is therefore, nearly constant at all pressures.Gases, on the other hand exhibit a large variation in densities with pressure.

 

The density of water at 4°C (277 K) 1s

1.0 x 10° kg m™”. The relative density of a substance ia the ratio of its density to the density of water at 4°C. It is a dimensionless positive scalar quantity. For example the relative

density of aluminium is 2.7. Its density is 2.7 x 107 kgm ™ The densities of some common fluids are displayed in Table 10.1.

 

Exampte 10.1 The two thigh bones

(femurs), each of cross-sectional area 10 cm? support the upper part of a human body of niass 40 kg. Estimate the average pressure sustained by the femurs.

Answer Total cross-sectional area of the

femurs is A = 2 x 10 cm? = 20 x 10* m*. The force acting on them is F = 40 kg wt = 400 N (taking g = 10 m 8°. This force is acting vertically down and hence, normally on the femurs. Thus, the average pressure is F.. 5 yy yee

Par = = 2210 Na <

 

10.2.1 Pascal's Law

The French scientist Blaise Pascal observed that the pressure in a flufd at reat is the same at all points if they are at the same height. This fact

may be demonstrated in a simple way.

Ng. 10.2 shows an element in the interior of a fluid at rest. This element ABC-DEF is in the form of a right-angled prism. In principle, this

prismatic element is very small ao that every part of it can be considered at the same depth from the liquid surface and therefore, the effect of the gravity is the same at all these points.

But for clarity we have enlarged this element.The forces on this element are those exerted by the reat of the fluid and they must be normal to the surfaces of the element as discussed above.

Thus, the fluid exerts pressures P,, PF and Pon

 

this element ofarea corresponsing to the normal forces F., F, and F, as shown in Fig. 10.2 on the facea BEFC, ADFC and ADEB denoted by A,, A,and A, respectively. Then Fysing@=F, F,coaQ=F, (by equilibrium)A,aing=A, A,coat= A, (by geometry)Thua,FoF Fi.A, AL A, P, = P. = P, (10.4)

 

Hence, pressure exerted is same in all

directions in a fliid at reat. It again reminds us that like other typea of stress, pressure is not a vector quantity. No direction can be assigned

to it. The force against any area within (or bounding) a fluid at rest and under pressure is normal to the area, regardleas of the orfentation

of the area.

 

Now consider a fluid element in the form ofa hortzonial bar of uniform cross-section. The bar is in equilfbrium. The horizontal forces exerted at its two ends muat be balanced or the

pressure at the two ends should be equal. This proves that for a liquid in equilibrium the pressure is same at all points in a horizontal plane. Suppose the pressure were not equal in

different parts of the fluid, then there would be flow as the fluid will have some net force acting on ft. Hence in the absence of flow the pressure in the fliiid must be same everywhere.Wind is flow of air due to pressure differences.

10.2.2 Variation of Preasure with Depth

Consider a fluid at rest in a container. In Ng. 10.3 point 1 is at height h above a point 2.The pressures at points 1 and 2 are P, and P,respectively. Consider a cylindrical element of fluid having area of base A and height h. As the fluid is at reat the resultant horizontal forces should be zero and the resultant vertical forces should balance the weight of the element. The forces acting in the vertical direction are due to

the fluid preasure at the top (PA) acting downward, at the bottom (P,A) acting upward.If mg is weight of the fluid in the cylinder we have

(P,— P) A=mg (10.5)

 

Now, if p ia the mass density of the fluid, we have the mass of fluid to be m = pV= phA so that P,-P= pgh (10.6)

Presstre difference depends on the vertical distance h between the points (1 and 2), mass density of the fluid p and acceleration due to gravity g. If the point 1 under discussion ia shifted to the top of the fluid (say water), which is open to the atmosphere, P, may be replaced by atmospheric pressure (P,) and we replace P,by P. Then Eq. (10.6) gives P=P._+ pgh (10.7)

 

Thus, the pressure P, at depth below the

surface of a liquid open to the atmosphere is greater than atmospheric preasure by an amount pgh. The excess of pressure, P—P.. at depth his called a gauge pressure at that point.

 

The area of the cylinder is not appearing in the expression of absohute pressure in Eq. (10.7).Thus, the height of the fluid column is important

and not crass sectional or base arca or the shape of the container. The liquid pressure is the same at all points at the same horizontal level (same

depth). The result is appreciated through the example of hydrostatic paradox. Consider three vessels A, Band C [Fig.10.4] of different shapes.

They are connected at the bottom by a horizontal pipe. On filling with water the level in the three vessels is the same though they hold different

amounts of water. This is so, because water at the bottom has the same pressure below cach section of the vessel.

 

Example 10.2 What is the pressure on a

swimmer 10 m below the surface of a lake?

Answer Here h=10m and p = 1000 kg m*. Take g =10 ms" From Eq. (10.7)P=P,.+pgh

= 1.01 x 10° Pa + 1000 kg mr x 10 ms*x 10m = 2.01 x 10° Pa « 2 atm

 

This is a 100% increase in pressure from

surface level. At a depth of 1 km the increase in pressure is 100 atm! Submarines are designed to withstand such enormous pressures. <10.2.8 Atmospheric Pressure and Gauge

 

Pressure

The pressure of the atmosphere at any point is equal to the weight of a column of air of unit cross sectional area extending from that point to the top of the atmosphere. At sea level it is

1.013 x 10° Pa (1 atm). Italian scientist Evangelist a Torricelli (1608-1647) devised for the first time, a method for measuring atmospheric pressure. A long glass tube closed

at one end and filled with mercury is inverted into a trough of mercury as shown in Fig. 10.5 (a).This device is known as mercury barometer. The

space above the mercury cohumn in the tube contains only mercury vapour whose pressure P is so small that it may be neglected. The pressure inside the column at point A must equal the pressure at point B, which is at the

same level. Pressure at B = atmospheric

pressure = P P.=pgh (10.8)where p is the density of mercury and h is the height of the mercury column in the tube.

 

In the experiment it is found that the mercury column in the barometer haa a height of about 76cm at sea level equivalent to one atmosphere (1 atm). This can alse be obtained using the

value of p in Eq. (10.8). A common way of stating pressure is in terma of cm or mm of mercury (Hg). A pressure equivalent of 1 mm is called a torr (after Torricelli).1 torr = 133 Pa.

 

The mm of Hg and torr are used in medicine and physiology. In meteorology, a common unitis the bar and millibar.

1 bar = 10° Pa

 

An open-tube manometer is a useful

instrument for measuring pressure differences.It consists of a U-tube containing a suitable Hiquid Le. a low density liquid (auch as off) for

measuring small pressure differences and a high density liquid (such as mercury) for large pressure differences. One end of the tube is open to the atmosphere and other end is connected to the syatem whose pressure we want to measure [see Fig. 10.5 (b)]. The pressure Pat A

ja equal to preasure at point B. What we

normally measure is the gauge pressure, which is P- P., given by Eq. (10.8) and is proportional to manometer height fh.

 

Pressure is same at the same level on both sides of the U-tube containing a fluid. For liquide the density varies very lttile over wide Tanges in pressure and temperature and we can treat it safely as a constant for our present

purposes. Gases on the other hand, exhibits large variations of densities with changes in pressure and temperature. Unlike gases, liquids

are therefore, largely treated aa tncompresatble.

 

Example 10.3 The density of the

atmosphere at sea level is 1.29 kg/m.

Assume that it does not change with

altitude. Then how high would the

Answer We use Eq. (10.7)pgh = 1.29kgm®>x9.6ms?xh m=1.01x10°Pa

h= 7989 m = 8 km

 

In reality the density of air decreasea with height. So does the value of g. The atmospheric cover extends with decreasing pressure over 100 km. We should also note that the sea level

atmospheric pressure is not always 760 mim of Hg. Adrop in the Hg level by 10 mm or more is a sign of an approaching storm.

 

Example 10.4 At a depth of 1000 m inan

ocean (a) what is the absolute pressure?

(b) What is the gauge pressure? (c) Find

the force acting on the window of area

20 cm x 20 cm of a submarine at this

depth, the interior of which is maintained at sea-leve] atmospheric pressure. (The density of sea water is 1.03 x 10° kg m5,g= 10m s7,)

Answer Here h= 1000 m and p=1.03x 10° kgm*.

(a) From Eq, (10.6), absolute pressure

P=P,+pgh

= 1.01 x 10° Pa

+ 1.03 x 10°kg m® x 10 ms?x 1000 m

= 104.01 x 10’ Pa

= 104 atm

 

(b) Gauge pressure is P-P._= pgh = P

P, = 1.03 x 10° kg nr°x 10 ms? x fooo m

= 103 x 10° Pa 103 atm

 

(c) The pressure outside the submarine is P=P_+ pgh and the pressure inside it is P.. Hence, the net pressure acting on the window is gauge pressure, P, = pgh. Since the area of the window is A= 0.04 m?’, the force acting on it is

F=P,A=108x 10°Pax0.04m?=412x 10°N

 

10.2.4 Hydraulic Machines

Let us now consider what happens when we

change the pressure on a fluid contained in a vessel. Consider a horizontal cylinder with a piston and three vertical tubes at different points. The pressure in the horizontal cylinder

is indicated by the height of liquid column in the vertical tubes.It is necessarily the same in all. If we push the piston, the fluid level rises in

all the tubes, again reaching the same level in each one of them.

 

This indicates that when the pressure on

the cylinder was increased, it was distributed uniformly throughout. We can say whenever external pressure is applied on any part of a fiaid contained in a veseel, it is transmitted

undiminished and equally in all directions.This is the Pascal’s law for transmission of fluid pressure and has many applications in daily life.

 

Anumber of devices such as hydraulic lift and hydraulic brakes are based on the Pascal's law. In these devices fluids are used for transmitting pressure. In a hydraulic lift as

shown in Fig. 10.6 two pistons are separated by the space filled with a liquid. A piston of small cross section A, is used to exert a force F,F,

directly on the liquid. The pressure P= 7] is transmitted throughout the liquid to the larger cylinder attached with a larger piston of area A,which results in an upward force of P x A,.Therefore, the piston is capable of supporting a

large force (large weight of, say a car, or a truck,FA,placed on the platform) F,= PA, = “A * By changing the force at A,, the platform can be Ftuid appears to provide partial support to the objecta placed in it. When a body is wholly or partially immersed in a fhud at rest, the fluid exerts pressure on the surface of the body in contact with the fluid. The pressure is greater on lower surfaces of the body than on the upper surfaces as pressure in a fluid increases with depth. The resultant of all the forces is an upward force called buoyant force.Suppose that a cylindrical body is immersed in the fluid. The upward force on the bottom of the body

is more than the downward force on its top. The fluid exerts a resultant upward force or buoyant force on the body equal to (P,-P,) A We have seen in equation 10.4 that (P,-P,A = pghA. Now hA is the

volume of the solid and phAis the weight of an equiveliant volume of the fhuid. (P,-P,)A = mg. Thus the upward force exerted is equal to the weight of the displaced fhud.

 

The result holds true irrespective of the shape of the object and here cylindrical object is considered

only for convenience. This is Archimedes’ principle. For totally immersed objects the volume of the

fluid displaced by the object is equal to ita own voliume. If the density of the immersed object is more than that of the fluid, the object will sink as the weight of the body is more than the upward thrust. If the denaity of the object is less than that of the fluid, it floats in the fhud partially submerged. To calculate the volume submerged. Suppose the total volume of the abject is V. and a part V of it is

submerged in the fhud. Then the upward force which is the weight of the displaced fluid is pgV,.which must equal the weight of the body: p,gV, = pgVior p/p, = V/V, The apparent weight of the

floating body is zero.

 

This principle can be summarised ag; ‘the loss of weight of a body submerged (partially or fully) in a fluid is equal to the weight of the fluid displaced’.

moved up or down. Thus, the applied force has A,been increased by a factor of “3. and this factor is the mechanical advantage of the device. The example below clarifies it.

Example 10.5 Two syringes of different cross sections (without needles) filed with

water are connected with a tightly fitted rubber tube filled with water. Diameters of the smaller piston and larger piston are 1.0 cm and 3.0 cm respectively. fa) Find the force exerted on the larger piston when a force of 10 N is applied to the smaller piston. (b) If the smaller piston is pushed

in through 6.0 cm, how much does the

larger piston move out?

Answer (a) Since pressure is transmitted

undiminished throughout the fluid,

n(3/2x10%m)F, =f: p _2(8/2%10%m) 10N

A, a(1/2x107 m)=90N

 

(b) Water is considered to be perfectly

incompressible. Volume covered by the

movement of smaller piston inwards is equal to vohime moved outwards due to the larger piston.

LA, = LA,

x(1/2x 10% m)

L, -AL _2(1/2%10" m) 6 x107%m

A, n(3/2x 10m)

= 0.67 x 107m = 0.67 cm

 

Note, atmospheric pressure is common to both pistons and has been ignored. <

Example 10.6 In a car lift compreased air exerts a force F, on a small piston having a radius of 5.0 cm. This pressure is transmitted to a second piston of radiua 15 cm (Fig 10.7). If the mass of the car to be lifted is 1350 kg, calculate F- What is the pressure necessary to accomplish this task? (g = 9.8 ms4.

Answer Since pressure is transmitted

undiminished throughout the fluid,

A (5x 107m) ot F, =—1 F, = ———_—_,(1850 Nx 9.8 ms*] A, m(15x 107m)=1470N

#15x10°N The air pressure that will produce this force is P ~~ _15*10N ig x10°Pa A, x(5x107) m

 

This is almost double the atmospheric

pressure.Hydraulic brakes in automobiles also work on the same principle. When we apply a little p Archimedes (287 — 212 B.C.)oy Archimedes was a Greek philosopher, mathematician, scientist and engineer. He invented the catapult and devised a aystem of pulleys and levers to handle heavy wk, loads. The king of bis native city Syracuse, Hiero II asked htm to determine ff his gold

i. - -@ crown was alloyed with some cheaper metal such as aitver without damaging the crown.The partial loss of weight he experienced while lying in his bathtub suggested a aolution te him. According to legend, he ran naked through the streeta of Syracuse exclaiming “Eureka,eureka!", which meana "I have found tt, I have found it!"

force on the pedal with our foot the master piston moves inside the master cylinder, and the pressure caused is transmitted through the brake ofl to act on a piston of larger area. A

large force acts on the piston and is pushed down expanding the brake shoes against brake lining. In this way a small force on the pedal produces a large retarding force on the wheel.

An important advantage of the system is that the pressure set up by pressing pedal is transmitted equally to all cylinders attached to the four wheels so that the braking effort is equal on all wheels.

 

10.3 STREAMLINE FLOW

So far we have stndied fluids at rest. The study of the fluids in motion is known as fluid dynamics. When a water-tap is turned on slowly, the water flow ia smooth initially, but loses its smoothness when the speed of the

outflow is increased. In studying the motion of fluids we focus our attention on what is happening to various fluid particles at a particular point in space at a particular time.The flow of the fluid is aaid to be steady if at

any given point, the velocity of each passing fluid particle remains constant in time. This does not mean that the velocity at different points in space is same. The velocity of a particular particle may change as it moves from

one point to another. That is, at some other paint the particle may have a different velocity, but every other particle which passes the second

point behaves exactly as the previous particle that has just passed that point. Each particle follows a smooth path, and the paths of the particles do not cross each other.

 

The path taken by a fluid particle under a steady flow is a streamline. It is defined as a curve whose tangent at any point is in the direction of the fluid velocity at that point.Consider the path of a particle as shown in Fig.10.7 (a), the curve describes how a fluid

particle moves with time. The curve PQ is like a permanent map of fhuid flow, indicating how the fhiid streams. No two streamlines can cross,for if they do, an oncoming fluid particle can go either one way or the other and the flow would not be steady. Hence, in steady flow, the map of flow is stationary in time. How do we draw closely spaced streamlines ? If we intend to show

streamline of every flowing particle, we would end up with a continuum of lines. Consider planes perpendicular to the direction of fluid flow e.g., at three points P, R and Q in Fig.10.7 {b).

The plane pieces are so chosen that their boundaries be determined by the same sect of streamlines. This means that number of fluid particles crossing the surfaces as indicated at P, Rand Q is the same. Ifarea of cross-sections

at these points are A,,A, and A, and speeds of fhild particles are v,, v, and u,. then mass of fluid Am, crossing at A, in a small interval of time At is p,A,v, At. Similarly mass of fluid am,

flowing or crosaing at A, in a small interval o time At is p,A,v, At and mass of fluld Am, is p,A.u, At crossing at A,. The mass of liquid ad out equals the masa flowing in, holds in all cases. Therefore,pA At = p,A,u,At= Pulte At (10.9)For flow of incompressib fuids

Pp= Pa =P Equation (10.9) reduces to

A,v, = AD, = Agu, (10.10)

which is called the equation of continuity and itis a statement of conservation of mass tn flow of incompressible fluids. In general

Av = constant (10.11)

Av gives the volume flix or flow mate and remains constant throughout the pipe of flow.Thus, at narrower portions where the streamlines are closely apaced, velocity increases and its vice versa. From (Fig 10.7b) it ia clear that A, > Alor uv, < w,, the fhnid is accelerated while passing from K to Q. This is

associated with a change in pressure in fluid flow in horizontal pipes.

Steady flow is achieved at low flow apeeda.Beyond a limiting value, called critical speed,thia flow loses steadiness and becomes turbnlent. One secs this when a fast flowing stream encounters rocks, small foamy whirlpool-like regions called ‘white water rapids are formed.

 

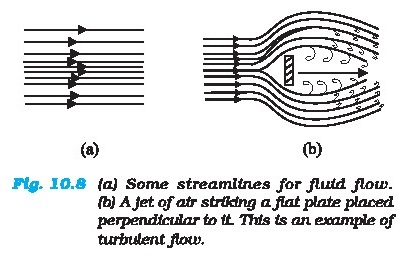
Figure 10.8 displays streamlines for some typical flows. For example, Fig. 10.8(a) describes a laminar flow where the velocities at different points in the fluid may have different magnitudes but their directions are parallel.

Figure 10.8 (b) gives a sketch of turbulent flow.

 

10,4 BERNOULLI'S PRINCIPLE

Fluid flow is a complex phenomenon. But we can obtain some useful properties for steady or streamline flows using the conservation of energy.

 

Consider a fluid moving in a pipe of varying cross-sectional area. Let the pipe be at varying heights as shown in Fig. 10.9. We now suppose that an incompressible fluid is flowing through

the pipe in a steady flow. Ite velocity must change as a consequence of equation of continuity. A force is required to produce this acceleration, which is caused by the fluid surrounding it, the pressure must be different in different regions. Bernoulli's equation is a

general expression that relates the pressure difference between two points in a pipe to both velocity changes (kinetic energy change) and elevation (height) changes {potential energy

change). The Swiss Physicist Daniel Bernoulli developed this relationship in 1738.

 

Consider the flow at two regions 1 (1.c. BC)and 2 (.c. DE). Consider the fud initially lying between B and D. In an infinitesimal time interval At, this fluid would have moved.Suppose v, ia the speed at B and v, at D, then

fluid initially at B has moved a distance v,At to C (v,At is small enough to assume constant cross-section along BC). In the same interval At the fluid initially at D moves to E, a distance

equal to v,Af. Pressures P, and P, act as shown on the plane faces of areas A, and A, binding the two regions. The work done on the fluid at left end (BC) is W, = P.A(v,A6 = PAV. Since the same volume AV passes through both the regions (from the equation of continuity) the work done by the fluid at the other end (DE) is W, = P,A,(v,A0 = P,AV or, the work done on the fluid is =P,AV. So the total work done on the fluid is W, - W,= (P,- P) AV

 

Part of this work goes into changing the kinetic energy of the fluid, and part goes into changing the gravitational potential energy. If the density

of the fluid is p and Am = pAv,At = pAV is the mass passing through the pipe in time Ai, then change in gravitational potential energy is AU = pgAV (h,- hh)

 

The change in tte kinetic energy is

1 AK= (3) p AV (,?- u,3]

We can employ the work — energy theorem

{Chapter 6) to this volume of the fluid and this yields

1 (P- P) AV= (3) p AV (u,2- v,)) + poAV (h,- A)We now divide each term by AV to obtain 1 {P- P) = (5) p (v,7- v4) + Pg (h,- h)

 

Dantel Bernoulli (1700-1782)

-— ( ‘ Daniel Bernoulli was a Swiss sdentist and mathematician who along with Leonard “4 3 Euler had the distinction of winning the French Academy prize for mathanatics

a ten times. He also studied medicine and served as a professor of anatomy and

iia SS a botany for a while at Basle, Switzerland. His most well known work was in és i ara hydrodynamics, a subject he developed from a aingle principle: the conservation . Lae of energy. His work included calculus, probability, the theory of vibrating strings,and applied mathematics. He has been called the founder of mathematical physics.

 

We can rearrange the above terms to obtain 1 1 P+ (5) po,? + pgh, = P+ (=) pu, + pgh,(10.12)

 

This is Bernoulli’s equation. Since 1 and 2 refer to any two locations along the pipeline,we may write the expression in general as 

P+ (= ow + pgh = constant (10.13)In words, the Bernoulli’s relation may be stated as follows: As we move along a streamline the sum of the pressure (P), the kinetic energy

v per unit volume a and the potential energy per unit volume (pgh) remains a constant.Note that in applying the energy conservation principle, there is an assumption that no energy is lost due to friction. But in fact, when fluids

flow, some energy does get lost due to internal friction. This arises due to the fact that in a fluid flow, the different layers of the fluid flow

with different velocities. These layera exert frictional forces on each other resulting in a loss of energy. This property of the fluid is called

viscosity and is discussed in more detail in a later section. The lost kinetic energy of the fluid

geta converted into heat energy. Thus,

Bernoulli's equation ideally applies to fluids with zero viscosity or non-viscous fluids. Another restriction on application of Bernoulli theorem

fs that the fluids must be  incompressible, as the elastic energy of the fluid is also not taken into consideration. In practice, it has a large number of useful applications and can help explain a wide variety of phenomena for low viscosity incompressible fluids. Bernoulli's

equation also does not hold for non-steady or turbulent flows, because in that situation velocity and pressure are constantly fluctuating in time.

 

When a fluid is at rest i.e. tts velocity is zero everywhere, Bernoulli's equation becomes P, + pgh, = P, + pgh,

(P- P) =pg th,-h)which is same as Eq. (10.6).

10.4.1 Spesd of Efflux: Torricelli’s Law

The word efflux means fluid outilow. Torricelli discovered that the speed of efflux from an open tank is given by a formula identical to that ofa freely falling body. Consider a tank containing a liquid of density p with a small hole in its side at a height y, from the bottom (see Fig. 10.10).The air above the liquid, whose surface is at

height y,, is at pressure P. From the equation of continuity [Eq. (10.10)] we have uy, A, = vA,

by = AL v

27 Ay 1

 

If the cross sectional area of the tank A, is much larger than that of the hole (A, >>A,), then we may take the fluid to be approximately at Test at the top, i.e. v, = 0. Now applying the Bernoulli equation at points 1 and 2 and noting

that at the hole P, = P,, the atmospheric pressure, we have from Eq. (10.12)1s

Fut gee + egy =P +P gus

Taking U¥,— Y, = hwe have

2(P-P,)

v, = J2g n+ (10.14)

 

When P>>P,and 2 g h may be ignored, the

speed of efflux is determined by the container pressure. Such a situation occurs in rocket propulsion. On the other hand if the tank is open to the atmosphere, then P = P, and uyay2gh (10.15)This is the speed of a freely falling body.Equation (10.15) is known as Torricelli's law.

 

10.4.2 Venturi-meter

The Venturi-meter ia a device to measure the flow speed of incompressible fluid. It consists of a tube with a broad diameter and a small constriction at the middle as shown in Fig. (10.11). A manometer in the form of a U-tube ia also attached to it, with one arm at

the broad neck point of the tube and the other at constriction as shown in Fig. (10.11). The manometer contains a liquid of density p,. The speed, of the liquid flowing through the tube at the broad neck area A is to be measured from equation of continuity Eq. (10.10) the

__A speed at the constriction becomes , = Yy,Then using Bernoulli's equation, we get ‘1 1

Pt > pv,? = P+ > pv,? (A/a*

So that

at alfAY 4

P- P= DT pv,? [ al ] (10.16)

 

This pressure difference causes the fhuid in the U tube connected at the narrow neck to rise in comparison to the other arm. The difference in height h measure the pressure difference.

4 Ay ,

P-P,=p,gh= > pu,? al”

So that the speed of fluid at wide neck is

2p,.gh AY

v= i{ ? (2) ] (10.17)

 

The principle behind this meter has many

applications. The carburetor of automobile has a Venturi channel (nozzle) through which air flows with a large speed. The pressure fs then

lowered at the narrow neck and the petrol (gasoline) is sucked up in the chamber to provide the correct mixture of air to fuel necessary for combustion. Filter pumps or aspirators, Bunsen burner, atomisers and sprayers [See Fig. 10.12]used for perfiumes or to spray insecticides work on the same principle.

 

Example 10.7 Blood velocity: The flow

of blood in a large artery of an anesthetised dog is diverted through a Venturi meter.The wider part of the meter has a cross-sectional area equal to that of the artery.A= 8 mim’. The narrower part has an area a= 4mm’, The pressure drop in the artery is 24 Pa. What is the speed of the blood in

the artery?

Answer We take the density of blood from Table 10.1 to be 1.06 x 10° kg m*. The ratio of the areas is (2) = 2. Using Eq. (10.17) we obtain 2x24Pa -" | 1060 kg m™ x(2° - 1) O1eoms” 4

 

10.4.3 Blood Flow and Heart Attack

Bernoulli's principle helps in explaining blood flow in artery. The artery may get constricted due to the accumulation of plaque on its inner

walls. In order to drive the blood through this constriction a greater demand is placed on the activity of the heart. The speed of the flow of

the blood in this region is raised which lowers the pressure inside and the artery may collapse due to the external preasure. The heart exerts further pressure to open this artery and forces

the blood through. As the blood rushes through the opening, the internal pressure once again drops due to same reasons leading to a repeat collapse. This may reault in heart attack.

 

10.4.4 Dynamic Lift

Dynamic lift is the force that acts on a body,such as airplane wing, a hydrofoil or a spinning ball, by virtue of its motion through a fluid. In Many games such as cricket, tennis, baseball,

or golf, we notice that a spinning ball deviates from its parabolic trajectory as tt moves through air. This deviation can be partly explained on the basis of Bernoulli’s principle.

 

(i) Ball moving without spin: Fig. 10.13(a)shows the streamlines around a non-spinning ball moving relative to a fluid.From the symmetry of streamlines it is clear that the velocity of fhiid (air) above and below the ball at corresponding points is the same

resulting in zero pressure difference. The air therefore, exerts no upward or downward.force on the ball.

 

(i) Ball moving with spin: A ball which is spinning drags air along with it. If the surface is rough more air will be dragged. Fig 10.13(b) shows the streamlines of air for a ball which is moving and spinning at the same time. The ball is moving forward and relative to it the air is moving backwards. Therefore, the velocity of air

above the ball relative to ft is larger and below it is smaller. The stream Ines thus get crowded above and rarified below.

 

This difference in the velocities of air results in the pressure difference between the lower and upper faces and there is a net upward force on the ball. This dynamic lift due to spining is called Magnus effect.

Aerofoil or lift on aircraft wing: Figure 10.13

 

(c) shows an aerofoil, which is a solid piece shaped to provide an upward dynamic lift when it movea horizontally through air. The cross-section of the wings of an aeroplane looks somewhat like the aerofoil shown in Fig. 10.13 (c)with atreamlines around it. When the aerofoil moves against the wind, the orientation of the wing relative to flow direction causes the streamlines to crowd together above the wing more than those below it. The flow apeed on

top is higher than that below it. There is an upward force resulting in a dynamic lift of the wings and this balances the weight of the plane.

The following example illustrates this.

 

Example 10.8 A filly loaded Boeing

aircraft has a maas of 3.3 x 10° kg. Ita total wing area is 500 m?. It is in level flight with a speed of 960 km/h. (a) Estimate the pressure difference between the lower and upper surfaces of the wings (b)Estimate the fractional increase in the speed of the air on the upper surface of the wing relative to the lower surface. [The density of air is p = 1.2 kg mJ

Answer (a) The weight of the Boeing aircraft is balanced by the upward force due to the pressure difference

APxX A=3.3x 10° kg x 9.8 AP=(8.3 x 10° kg x 9.8m a4 / 500 m? = 6.5 x10* Nm?

 

(b) We ignore the small height difference between the top and bottom sides in Eq. (10.12).The pressure difference between them is then ap=E (uj - v7)where u, is the speed of air over the upper surface and v, is the apeed under the bottom surface.

(v, -v y= —2aP

27 88 8)

Taking the average speed

v,, = (v, + v,) /2 = 960 km/h = 267 m s*,‘we have (B; — B,)/ Bay ee 0.08

The speed above the wing needs to be only 8 % higher than that below.

 

10.5 VISCOSITY

Moat of the fhiids are not ideal ones and offer aome resistance to motion. This resistance to fhiid motion

is ike an ternal friction analogous to friction when.a aoltd moves on a surface. It is called viscosity.

This force exists when there is relative motion between layers of the liquid. Suppose we consider a fhiid Hike ofl enclosed between two glass plates

as shown in Fig. 10.14 (a). The bottom plate ts fixed while the top plate is moved with a constant velocity v relative to the fixed plate. If ofl is

replaced by honey, a greater force ia required to move the plate with the same velocity. Hence we say that honey is more viscous than oil. The fluid in contact with a surface has the same

velocity as that of the surfaces. Hence, the layer of the liquid in contact with top surface moves with a velocity w and the layer of the liquid in contact with the fixed surface is stationary. The

velocities of layers increase uniformly from bottom (zero velocity} to the top layer (velocity vj. For any layer of liquid, its upper layer pulls

it forward while lower layer pulls it backward.This results in force between. the layers. This type of flow ia known as laminar. The layers of liquid sHde over one another as the pages of a

book do when it is placed flat on a table and a hortzontal force is appled to the top cover. When a fluid is flowing in a pipe or a tube, then

velocity of the quid layer along the axis of the tube is maximum and decreases gradually as we move towards the walls where it becomes zero, Mig. 10.14 {b). The velocity on a cylindrical

surface in a tube is constant.

 

On account of this motion, a portion of liquid,which at some instant has the shape ABCD,take the shape of AEFD after short interval of time (AQ. During this time interval the liquid has undergone a shear strain of Ax/t Since, the strain in a flowing fluid increases with time continuously. Unlike a sold,here the stress is found experimentally to

depend on ‘rate of change of strain’ or ‘strain rate’ i.e. Ax/(LAQ or v/Linstead of strain itself.The coefficient of viacoaity (pronounced ‘eta) for

a fluid is defined as the ratio of shearing streas to the strain rate.

_ F/A Fl

TTL A (10.18)

 

The SI unit of viscosity is poiseiulle (PI). Its other units are N s m® or Pa s. The

 dimensions of viscosity are [ML"T"]. Generally thin liquids

Hike water, alcohol etc, are less viscous than thick liquids lfke coal tar, blood, glycerin etc.The coefficients of viscosity for some common fluids are listed in Table 10.2. We point out two facta about blood and water that you may find interesting. As Table 10.2 indicates, blood is ‘thicker’ (more viscous) than water. Further the

relative viscosity (y/n,,,,J of blood remains constant between O°C and 37°C,

 

The viscosity of liquids decreasea with

temperature while it increases in the case of gases.Example 10.9 A metal block of area 0.10 m?

$s connected to a 0.010 kg mass via a string that passes over an idea] pulley (considered massless and frictionless), as in Ng. 10.15.A liquid with a film thickness of 0.30 mm is placed between the block and the tabk.

 

When released the block moves to the right with a constant speed of 0.085 ms”. Find the coefficient of viscosity of the liquid.

Answer The metal block moves to the right because of the tension in the string. The tension T is equal in magnitude to the weight of the

suspended mass m. Thus the shear force F is F=T=mg=0.010 kg x 9.6m s7=9.8x 102N

Shear stress on the fluid = F/A = =~

‘v_0.085

Strain rate = 79 030

n= stress

strain rate

_(9.8x 10% N)(0.30 x10 m)

~ (0.085m s“)(0.10m?)

= 3.45 x10° Pas <

Table10.2 The viscositics of some fluids

10.6.1 Stokes’ Law When a body falls through a fluid it drags the layer of the fluid in contact with it. A relative

motion between the different layers of the fluid is set and as a result the body experiences a retarding force. Falling of a raindrop and swinging of a pendulum bob are some common examples of such motion. It is seen that the

viscous force is proportional to the velocity of the object and is opposite to the direction of motion. The other quantities on which the force F depends are viscosity 7, of the fluid and radius

a of the sphere. Sir George G. Stokes (1819-1903), an English scientist enunciated clearly the viscous drag force Fas F=6nnav (10.19)

 

This is known as Stokes’ law.We shall not derive Stokes’ law.This law is an interesting example of retarding

force which is proportional to velocity. We can study its consequences on an object falling through a viscous medium. We consider a raindrop in air. It accelerates initially due to gravity. As the velocity increases, the retarding

force also increases. Finally when viscous force plus buoyant force becomes equal to force due to gravity, the net force becomes zero and so does the acceleration. The sphere (raindrop)

then descends with a constant velocity. Thus in equilibrium, this terminal velocity v, is given by

 

Ganav, = (4x/3) a (p-o)g

where p and o are mass densities of sphere and the fluid respectively. We obtain u, = 2c? (p-a)g / (On) (10.20)

 

So the terminal velocity uv. depends an the square of the radius of the sphere and inversely on the viscosity of the medium.You may like to refer back to Example 6.2 in this context.

Example 10.10 The terminal velocity ofa

copper ball of radius 2.0 mm falling

through a tank of ofl at 20°C is 6.5 cm s?.

Compute the viscosity of the ofl at 20°C.Density of of] is 1.5 x10° kg m°, density of copper is 8.9 x 10° kg m®.

Answer We have v,= 8.5 x 10? ma’, a=2x 10° m.g=9.8 ms*, p = 8.9x 10° kg m*,

51.5 x10° kg m®. From Eq. (10.20)

; <3 2 2 qa 2 PLO x98 nT 107 }m = osm * x 7.4x 10° kg m~ 9 6.5x 107 ms

= 9.9x10'kgm's?

 

10.6 REYNOLDS NUMBER

When the rate of flow of a fluid is large, the flow no longer remain laminar, but becomes turbulent. In a turbulent flow the velocity of

the fhiids at any point in space varies rapidly and randomly with time. Some circular motions called eddies are also generated. An obstacle placed in the path of a fast moving fhiid causes

turbulence [Fig. 10.8 (b)]. The smoke rising from a burning stack of wood, oceanic currents are turbulent. Twinkling of stars ia the result of

atmospheric turbulence. The wakes in the water and in the air left by cara, aeroplanes and boats are also turbulent.

 

Osborne Reynolds (1842-1912) observed that turbulent. flow is less likely for viscous fluid flowing at low rates. He defined a dimensionless number, whose vahie gives one an approximate idea whether the flow would be turbulent . This number is called the Reynolds K,.

R= pud/n (10.21)

 

where p is the density of the fluid flowing with aspeed v, d stands for the dimension of the pipe, and 7 is the viscosity of the fluid. R, is a

dimensionless number and therefore, it remains same in any system of units. It is found that flow is streamline or laminar for R, less than 1000. The flow is turbulent for R. > 2000. The flow becomes unsteady for R, between 1000 and

2000. The critical value of R, (known as critical Reynokis number), at which turbulence sets, fs found to be the same for the geometrically similar flows. For example when of] and water with their different densities and viscosities, flow in pipes of same shapes and sizes, turbulence sets in at almost the same value of R,. Using this facta small scale laboratory model can be set up to study the character of fluid flow. They

are usefill in designing of ships, submarincs,racing cars and aeroplanes.

R, can also be written as R, = pw? / (qu/d) = pAv* f/ (nAo/d) (10.22)

= inertial force/force of viscosity.

 

Thus R, represents the ratio of inertial force (force duc to inertia 1.c. mass of moving fluid or due to inertia of obstacle in its path) to viscous

force.

 

Turbulence dissipates kinetic enemy usually in the form of heat. Racing cars and planes are engineered to precision tn order to minimise turbulence. The design of such vehicles involves

experimentation and trial and error. On the other hand turbulence (like friction) is sometimes desirable. Turbulence promotes mixing and increases the rates of transfer of mass, Momentum and energy. The blades of a kitchen mixer induce turbulent flow and provide thick milk shakes as well as beat eggs into a uniform texture.

 

Example 10.11 The flow rate of water from a tap of diameter 1.25 cm is 0.48 L/min.The coefficient of viscosity of water is 10° Pa a. After sometime the flow rate is increased to 3 L/min. Characterise the flow

Answer Let the speed of the flow be uv and the diameter of the tap be d = 1.25 cm. The volume of the water flowing out per second ia Q=uxnP/4 v=40/ da

We then estimate the Reynolds muimber to be R=4pO/ndy

=4 dO kg nr’x 9/8.14x1.25x10*m x10°Pas)

= 1.019 x 10° mr*s 9 Since initially

9=048L/ min=8 cm /s=8x 10° ms",

we obtain,R=815 Since this is below 1000, the flow is steady.After some time when Q=8L/ min=580 cm" /s=5x 10° m’s",

‘Wwe obtain,R = 5095

 

The flow will be turbulent. You may carry out an experiment in your washbasin to determine the transition from laminar to turbulent flow.

 

10.7 SURFACE TENSION

You must have noticed that, oil and water do not mix; water wets you and me but not ducks;mercury does not wet glass but water sticks to

it, ofl rises up a cotton wick, inspite of gravity,Sap and water rise up to the top of the leaves of the tree, hairs of a paint brush do not cling together when dry and even when dipped in water but form a fine tip when taken out of it.

All these and many more such experiences are related with the free surfaces of liquids. As liquids have no definite shape but have a definite volume, they acquire a free surface when poured in a container. These surfaces possess

some additional energy. This phenomenon is known as surface tension and it is concerned with only liquid as gases do not have free surfaces, Let us now understand this phenomena.

 

10.7.1 Surface Energy

A Hquid stays together because of attraction between molecules. Consider a molecule well inside a Hquid. The intermolecular distances are

such that it is attracted to all the surrounding molecules [Fig. 10,16{a)]. This attraction results in a negative potential energy for the molecule,

which depends on the number and distribution of molecules around the chosen one. But the average potential energy of all the molecules is

the same. This is supported by the fact. that to take a collection of such molecules (the liquid)and to disperse them far away from each other

in order to evaporate or vaporise, the heat of evaporation required is quite large. For water it is of the order of 40 kJ/mol.

 

Let us consider a molecule near the surface Fig. 10.16[b). Only lower half side of it is surrounded by liquid molecules, There is some negative potential energy due to these, but

obviously it is less than that of a molecule in bulk, Le., the one fully inside. Approximately it is half of the latter. Thus, molecules on a quid

surface have some extra energy in comparison to molecules in the interior. A liquid thus tends to have the least surface area which external conditions permit. Increasing surface area

requires energy. Most surface phenomenon can be understood in terms of this fact. What is the energy required for having a molecule at the surface? As mentioned above, roughly it is half the energy required to remove it entirely from

the liquid {.e., half the heat of evaporation.

 

Finally, what is a surface? Since a quid consists of molecules moving about, there cannot be a perfectly sharp surface. The density of the liquid

molecules drops rapidly to zero around z= 0 as we move along the direction indicated Fig 10.16 (c) in a distance of the order ofa few mokcular sizes.

 

10.7.2 Surface Energy and Surface Tension As we have discussed that an extra energy is associated with surface of liquids, the creation of more surface (spreading of surface) keeping

other things like volume fixed requires

additional energy. To appreciate this, consider a horizontal liquid film ending in bar free to slide over parallel guides Fig (10.17).

 

Suppose that we move the bar by a small

distance d as shown. Since the area of the surface increases, the system now has more energy, this means that some work haa been done against an internal force. Let this internal force be F, the work done by the applied force 1s F-d = Fit. From conservation of energy. this is stored as additional energy in the film. If the surface energy of the film is S per unit area,the extra area is 2dl. A film hae two sides and the liquid in between, so there are two surfaces

and the extra energy is S (2d) = Fu (10.23)Or, S=Fd/2dl = F/2t (10.24)

 

This quantity S is the magnitude of surface tension. It is equal to the surface energy per unit area of the Hquid interface and is also equal

to the force per unit length exerted by the fhiid on the movable bar.So far we have talked about the surface of

one liquid. More generally, we need to consider fhuid surface in contact with other fhutds or solid surfaces. The surface energy in that case depends on the materials on both sides of the

surface. For example, if the molecules of the materials attract each other, surface enemy is reduced while if they repe] each other the surface energy is increased. Thus, more appropriately, the surface energy is the energy of the interface between two materials and

depends on both of them.

 

We make the following observations from

above:

Surface tension is a force per unit length (or surface energy per unit area) acting in the plane of the interface between the plane of the liquid and any other substance; it also is the extra energy that the molecules at the interface have as compared to molecules

in the interior.

 

(i} At any point on the interface besides the boundary, we can draw a line and imagine equal and opposite sturface tension forces S per unit length of the line acting perpendicular to the line, in the plane of the interface. The line is in equilibrium. To be more spectiic, tmagine a line of atoms or molecules at the surface. The atoms to the left pull the line towards them; those to the right pull it towards them! This line of atoms is in equilibrium under tension. If the line really marks the end of the interface, as in Figure 10.16 (a) and (b) there is only the force S per unit length acting inwards.Table 10.3 gives the surface tension of various liquids. The value of surface tension depends

on temperature. Like viscosity, the surface tension of a liquid usually falls with temperature.

 

Table 10.3 Surface tension of some liquids at the temperatures indicated with the heats of the vaporisation

A fluid will stick to a solid surface if the surface energy between fluid and the solid is smaller than the sum of surface energies between solid-air, and fluid-air. Now there is cohesion between the solid surface and the liquid. It can be directly measured experimentaly as schematically shown in Fig.

 

10.18. A flat vertical glass plate, below which a vessel of some liquid is kept, forms one arm of the balance. The plate is balanced by weights on the other side, with its horizontal edge just over water. The vessel is raised slightly till the liquid just touches the glass plate and pulls it down a little because of surface tension. Weights are added till the plate just clears water.

 

Suppose the additional weight required is W.Then from Eq. 10.24 and the discussion given there, the surface tension of the liquid-air interface is

8, = (W/2) = Gng/20 (10.25)where m is the extra mass and Jis the length of

the plate edge. The subscript (la) emphasises the fact that the liquid-air interface tension is involved.

 

10.7.3 Angie of Contact

The surface of liquid near the plane of contact,with another medium is in general curved. The angle between tangent to the liquid surface at

the point of contact and solid surface inside the liquid is termed as angle of contact. It is denoted by @. It is different at interfaces of different pairs of liquids and solids. The value of @ determines whether a liquid will spread on the surface of a solid or it will form droplets on it. For example,

water forms droplets on lotus leaf as shown in Fig. 10.19 (a) while spreads over a clean plastic plate as shown in Fig. 10.19(b).

 

We consider the three interfacial tensions at all the three interfaces, liquid-air, solid-air and solid-liquid denoted by 8, S&S, respectively

as given in Fig. 10.19 (a) and (b). At the line of contact, the surface forces between the three media must be in equilibrium. From the Fig. 10.19(b) the

following relation is easily derived.

S,coad+ S = S. (10.26)

 

The angle of contact fa an obtuse angle if 5, > Sas in the case of water-leaf interface while it {s an acute angle if S, < S_ as in the case of water-plastic interface. When @ is an obtuse angle then molecules of liquids are attracted atrongly to themscives and weakly to

those of solid, tt costa a lot of energy to create a liquid-solid surface, and liquid then does not wet the solid. This is what happens with water on a waxy or oily surface, and with mercury on

any surface. On the other hand, if the molecules of the liquid are strongly attracted to those of the solid, this will reduce S, and therefore,cos @ may increase or 6 may decrease. In this

case @is an acute angle. This la what happens for water on glass or on plastic and for kerosene ofl on virtually anything (it just spreads). Soaps,

detergents and dying snbstances are wetting agents. When they are added the angle of contact becomes small so that these may penetrate well and become effective. Water proofing agents on the other hand are added to create a large angle of contact beween the water

and fibres.

 

10.7.4 Drops and Bubbles

One consequence of aurface tension ta that freeliquid drops and bubbles are spherical tf effects of gravity can be neglected. You must have seen this especially clearly in small drops fust formed tn a high-speed spray or jet, and in soap bubbles blown by most of us in childhood. Why are drops and bubbles spherical? What keeps soap bubbles stable?

 

As we have been saying repeatedly, a liquid-air interface has energy, so for a given volume the surface with mintmum energy is the one with the least area. The sphere has this property. Though it is out of the scope of this book, but you can check that a sphere is better

than at least a cube in this respectt So, tigravity and other forces (e.g. alr resistance} were ineffective, Hquid dropa would be spherical.

 

Another interesting consequence of surface tension is that the preasure fuside a spherical drop Fig. 10.20{a) is more than the presaure outside, Suppose a spherical drop of radius r is in equilibrium. If its radius increase by Ar. The extra surface energy is

[andr + Ar} 4- 4nr®] S = Ser Ar, (10.27}

If the drop is in equilibrium this energy cost is balanced by the energy gain due to expansion under the pressure difference (P.— P)between the inaide of the bubble and the outside. The work done isW = (P -P) 4nréar (10.28)

so that (R-P)=(2S/7 (10.29)

 

In general, for a liquid-gas interface, the convex side has a higher pressure than the concave aide. For example, an air bubble in a liquid, would have higher preasure inside it.See Fig 10.20 (b).A bubble Fig 10.20 (c) differs from a drop and a cavity; in thia it has two interfaces.Applying the above argument we have for a bubble (P-P)=4S/7 (10.30)

This is probably why yon have to blow hard,but not too hard, to form a soap bubble. A little extra air pressure is needed inside!

 

10.7.6 Capillary Rise

Qne consequence of the pressure difference acrogs a curved liquid-air interface is the well-known effect that water risea up in a narrow tube in spite of gravity. The word capilla means

hatr in Latin; if the tube were hair thin, the rise would be very large. To see this, consider a vertical capillary tube of circular cross section (radius a) Inserted into an open vessel of water

(Fig. 10.21). The contact angle between water and glass is acute. Thus the surface of water in the capillary is concave. This means that there ia a pressure difference between the

two sides of the top surface. This ia given by (P,- P) +2S/7 = 2S/{a sec 4)

=(2S/q) cos 8 (10.31)

 

Thus the pressure of the water inside the tube, just at the meniscus (air-water interface)is less than the atmospheric pressure. Consider

the two points A and B in Fig. 10.21(a). They must be at the same pressure, namelyP,+hpg=P=P, (10.32)where p is the density of water and h is called

the capillary rise [Fig. 10.21(a)]. Using Eq. (10.31) and (10.32) we have

hpg=(,- P) =(28 cos 0)/a (10.33)

 

The discussion here, and the Eqs. (10.28) and (10.29) make it clear that the capillary rise is due to surface tension. It is larger, for a smaller

a. Typically it is of the order of a few cm for fine capillaries. For example, if a = 0.05 cm, using the value of surface tension for water (Table 10.3), we find that h=2S/(pga

2 x(0.073 Nin}

(10°kg m™’)(9.8 ms~ }(5 x 107m)

= 2.98 x 107 m = 2.98 em

 

Notice that if the liquid meniscus is convex,as for mercury, Le., if cos 6 is negative then from Eq. (10.32) for example, it is clear that the

Hquid will be lower in the capillary !

10.7.6 Detergents and Surface Tension

We clean dirty clothes containing grease and oil stains sticking to cotton or other fabrics by adding detergents or soap to water, soaking clothes in it and shaking. Let us understand this process better.

 

Washing with water does not remove grease stains. This is because water does not wet greasy dirt; .e., there is very little area of contact between them. If water could wet grease, the

flow of water could carry some grease away.Something of this sort is achieved through detergents. The molecules of detergents are hairpin shaped, with one end attracted to water and the other to molecules of grease, oil or wax,thus tending to form water-ofl interfaces. The result is shown in Fig. 10.22 as a sequence of figures.In our language, we would say that addition of detergents, whose molecules attract at one end and say, oil on the other, reduces  drastically the surface tension S fwater-oil}. It may even become energetically favourable to form such

interfaces, i.c., globs of dirt surrounded by detergents and then by water. This kind of process using surface active detergents or surfactants is tmportant not only for cleaning,

but also in recovering oil, mineral ores etc.

 

Exampie 10,12 The lower end of a capillary tube of diameter 2.00 mm is dipped 8.00 cm below the surface of water in a beaker.What is the pressure required in the tube in order to blow a hemispherical bubble at tts end in water? The surface tension of water at temperature of the experiments is

7.30 x10 Nm}.1 atmospheric pressure = 1.01 x 10° Pa,density of water = 1000 kg/m*, ¢ = 9.80 m s?.Also calculate the excess pressure.Answer The excess pressure in a bubble of gas in a liquid is given by 2S/r, where S is the

surface tension of the liquid-gas interface. You should note there is only one liquid surface in this case. (For a bubble of liquid in a gas, there

are two liquid surfaces, so the formula for excess pressure in that case is 4S/r) The radius of the bubble is r. Now the pressure outside the bubble P, equals atmospheric pressure plus the

pressure due to 8.00 cm of water column. That is P= (1.01 x 10° Pa + 0.08 m x 1000 kg m®

x 9.80 m 84)

= 1.01784 x 10° Pa

Therefore, the pressure inside the bubble is

P =P, +28/r

= 101764 10° Pa+(2x7.3x 102Pam/10°m)

= (1.01784 + 0.00146) x 10% Pa

= 1.02 x 10° Pa

 

where the radius of the bubble is taken to he equal to the radius of the capillary tube, since the bubble is hemispherical | (The answer has

been rounded off to three significant figures.)The excess pressure in the bubble is 146 Pa. <4

 

SUMMARY

1. The basic property of a fluid is that tt can flow. The fluid does not have any

resistance to change of its shape. Thus, the shape of a fluid is governed by the

shape of its container.

 

2. Aliquid is ncompressible and hae a free surface of its own. A gas is compressible and it expands to occupy all the apace available to it.

 

3. ‘If Fis the normal force exerted by a fluid on an area A then the average pressure P., ia defined as the ratio of the force to area P, -7

 

4. The unit of the pressure is the pascal (Pa). It is the same as N m’. Other common units of pressure are

1 atm = 1.01x10° Pa

1 bar = 10° Pa

1 torr = 133 Pa = 0.133 kPa

1 mm of Hg = 1 torr = 133 Pa

 

5.  Pascat’s taw states that: Preasure in a fluid at rest is same at all points which are at the same height. A change in preasure applied to an enclosed fhud is tranamitied undiminished to every point of the fluid and the walla of the containing veasel,

 

6. The pressure in a fluid varies with depth bh according to the expression.

Pe P+pgh where . o the denaity of the fluid, assumed uniform.

 

7. The volume of an incompressible fluid passing any point every second in a pipe of non uniform crossection is the same in the steady flow,vA= constant ( vis the velocity and A is the area of crossection)The equation is due to mass coneervation in incompresaible fuid flow.

 

8. Bernoulli's principle states that as we move along a streamline, the sum of the presaure (7), the kinetic energy per unit volume (p¢/2) and the potential energy per unit volume (gif remains a constant,P+ pv4/2 + pgy = constant

The equation is basically the conservation of energy applied te non viacuse fluid motion in steady state. There is no fluid which have zero viacostty, so the above statement ia true only approximately. The viacoaity is like friction and converts the

kinetic energy to heat energy.

 

9. Though shear strain in a fluid does not require shear stress, when a shear stress is applied to a fluid, the motion is generated which causes a shear strain growing with time. The ratio of the shear streaa to the time rate of shearing strain is known af coefficient of viscoaity,.where symbols have their usual meaning and are defined in the text.

 

10. Stokes’ law states that the viscous drag force F on a sphere of radius a moving with velocity v through a fluid of viscosity ia, F = - Grnav.

 

11. The onset of turbulence in a fluid is determined by a dimensionless parameter is called the Reynolds number given by R, = pod/y Where dia a typical geometrical length associated with the fluid flow and the other symbols have their usual meaning.

 

12. Surface tension is a force per unit length (or surface energy per unit area) acting in the plane of interface between the liquid and the bounding surface. It is the extra energy that the molecules at the interface have as compared to the interior.

 

POINTS TO PONDER

1. Pressure is a scalar quantity. The definition of the pressure as “force per unit areca”mnay give one falac impression that pressure is a vector. The “force” in the numerator

of the definition is the component of the force normal to the arca upon which it fa impressed. While describing fluids as a conceptual shift from particle and rigid body mechanics ia required. We are concerned with properties that vary from point to point in the fluid.

 

2. One should not think of pressure of a fluid as being exerted only on a solid like the walls of a container or a piece of solid matter immersed in the fluid. Pressure exists at all points in a fluid. Anu element of a fluid {such as the one shown in Fig. 10.2) is in

equilibrium because the pressures exerted on the various faccsa are equal.

 

3. The expression for pressure

P= P.+pgh holds tric if fluid is incompreseible. Practically speaking it holds for liquids, which are largely incompresaible and hence {a a constant with height.

 

4. The gauge pressure is the difference of the actual pressure and the atmospheric pressure.P-P.=P,Many pressure-measuring devices measure the gauge pressure. These include the

tyre pressure gauge and the blood pressure gauge (sphygmomanometer).

 

5. A streamline is a map of fhiid flow. In a steady flow two streamlines do not intersect as it means that the fluid particle will have two posaible velocities at the point.

 

6. Bemmoull’s principal docs not hold in presence of viscous drag on the fluid. The work done by this diseipative viscous force must be taken into account in this case, and P,[Fig. 10.9] will be lower than the value given by Eq. (10.12).

 

7. As the temperature rises the atoms of the liquid become more mobile and the coeffiident of viscosity, n. falls. In a gas the temperature rise increascs the random motion of atoms and 1 increases.

 

8. The critical Reynolds number for the onset of turbulence is in the range 1000 to 10000, depending on the geometry of the flow. For most cases R, < 1000 signifies laminar flow, 1000 < R, < 2000 is unetcady flow and R, > 2000 implies turbulent flow.

 

9. Surface tension arises duc to cxcess potential energy of the molecules on the surface in comparison to their potential energy in the interior. Such a surface margy is present at the interface separating two substances at least one of which is a fhud. It is not the

property of a single fluid alone.

 

EXERCISES

10.1 Explain why

(a) The blood pressure in humans is greater at the feet than at the brain

 

(b) Atmospheric pressure at a height of about 6 km decreases to nearly half of

its value at the sea level, though the height of the atmosphere is more than

100 km

 

(c) Hydrostatic pressure is a scalar quantity even though pressure is force

divided by area.

 

10.2 Explain why

(a) The angle of contact of mercury with glass is obtuse, while that of water

with glass is acute.

 

(b) Water on a clean glass surface tends to spread out while mercury on the

same surface tends to form drops. (Put differently, water wets glass while

mercury does not.)( Surface tension of a liquid ts independent of the area of the surface

 

(@) Water with detergent disolved in it should have small angles of contact.

 

() Adrop of liquid under no external forces is always spherical in shape

 

10.3 Fill in the blanks using the word(s} from the Het appended with each statement:

 

(a) Surface tension of liquids generally ... with temperatures (increases /

decreases)

 

(b) Viscosity of gases ... with temperature, whereas viscosity of liquide ... with temperature (increases / decreases)

 

(For solids with elastic modulus of rigidity, the shearing force is proportional to... . while for fluids it is proportional to ... (shear strain / rate of shear strain)

 

@) For a fluid in a steady flow, the increase in flow speed at a constriction follows (conservation of mass / Bernoulli's principle)

 

() For the mode of a plane in a wind tunnel, turbulence occurs at a ... speed for turbulence for an actual plane (greater / smaller)

 

10.4 Explain why

(a) To keep a piece of paper horizontal, you should blow over, not under, it

 

(b) When we try to close a water tap with our fingers, fast jete of water gush through the openings between our fingers

 

(The aize of the needle of a syringe controls flow rate better than the thumb

pressure exerted by a doctor while administering an injection

 

(@) A uid Dowing cut of a small hole in a vessel results in a backward thrust on

the vessel

 

() Aspinning cricket ball in air does not follow a parabolic trajectory

 

10.5 ASO kg girl wearing high heel shoes balances on a single heel. The heel is circular with a diameter 1.0 cm. What is the pressure exerted by the heel on the horizcntal floor ?

 

10.6  Toricelli's barometer used mercury. Pascal duplicated it using French wine of density 964 kg m™. Determine the height of the wine column for normal atmospheric pressure.

 

10.7 A vertical off-shore structure is built to withstand a maximum stress of 10° Pa. Is the structure suitable for putting up on top of an ofl well m the ocean ? Take the depth of the ocean to be roughly 3 km, and ignore ocean currents.

 

10.8 A hydraulic automobile lift is designed to lift cars with a maximum mass of 3000 kg. The area of cross-section of the piston carrying the load is 425 cm*, What Maximum pressure would the smaller piston have to bear?

 

10.9 AU-tube contains water and methylated spirit separated by mercury. The mercury cohimne in the two arma are in level with 10.0 cm of water in one arm and 12.5 cm of spirit in the other. What fs the specific gravity of spirit?

 

10.10 In the previous problem, ff 15.0 cm of water and spirit each are further poured into the reapective arms of the tube, what is the difference in the levels of mercury m the two arms ? (Specific gravity of mercury = 13.6)

 

10.11 Can Bernoulli's equation be used to describe the flow of water through a rapid in a river ? Explain.

 

10.12 Does tt matter if one uses gauge instead of absolute pressures in applying Bernoulli's equation ? Explain.

 

10.13 Glycerine flows steadily through a horizontal tube of length 1.5 m and radius 1.0 cm. If the amount of glycerine collected per second at one end fs 4.0 x 10° kg 5",what is the pressure difference between the two ends of the tube? (Denaity of glycerine = 1.3 x 107 kg m™ and viscosity of glycerine = 0.83 Pa a). [You may also like to check if the assumption of laminar flow in the tube is correct].

 

10.14 In a test experiment on a model aeroplane in a wind tunnel, the flow speeds on the upper and lower surfaces of the wing are 70 m sand 63 m s” respectively. What is the lift on the wing ff its area is 2.5 m* ? Take the denaity of air to be 1.3 kg m™®.

 

10.15 Figures 10.23{a) and (b) refer to the steady flow of a (non-viscous) Hquid. Which of the two figures is incorrect ? Why ?

 

10.16 The cylindrical tube of a spray pump hase a crose-section of 8.0 an? one end of which has 40 fine holea each of diameter 1.0 mm. If the liquid flow inside the tube is 1.5 m min, what is the speed of ejection of the liquid through the holes?

 

10.17 A U-shaped wire is dipped in a soap solution, and removed. The thin soap film formed between the wire and the Hght slider supports a weight of 1.6 x 107 N (which includes the small weight of the slider). The length of the slider is 30 cm.What is the surface tension of the film ?

 

10.18 Figure 10.24 (a) shows a thin liquid film supporting a small weight = 4.5 x 107 N.What is the weight supported by a film of the same liquid at the same temperature in Fig. (b) and (c) ? Explain your answer physically.

 

10.19 What is the pressure inside the drop of mercury of radius 3.00 mm at reom temperature ? Surface tension of mercury at that temperature (20 °C) is 4.65 x 107 Nm”. The atmospheric presaure is 1.01 x 10° Pa. Also give the excess pressure inside the drop.

 

10.20 What is the pressure inside a bubble of soap solution of radius 5.00 mm,given that the surface tension of soap sohution at the temperature (20 °C) ia 2.50 x 107 N m '? If an atr bubble of the same dimension were formed at depth of 40.0 ci inside a container containing the soap solution (of relative density 1.20), what would be the preseure inside the bubble ? (1 atmospheric pressureis 1.01 x 10° Pa).

 

Additional Exercises

10.21 A tank with a square base of area 1.0 m? fs divided by a vertical partition in the middle. The bottom of the partition has a emall-hinged door of area 20 cm*. The tank is filled with water in one compartment, and an acid (of relative density 1.7)in the other, both to a height of 4.0 m. compute the force necessary to keep the door close.

 

10.22 Amanometer reads the pressure of a gas in an enclosure as shown in Fig. 10.25 (a)‘When a pump removes some of the gan, the manometer reads as in Fig. 10.25 (b)The Hquid used in the manometers ia mercury and the atmospheric pressure is 76 cm of mercury.a) Give the absolute and gauge preasure of the gas in the enclosure for cases (a) and (b), in units of cm of mercury.(b) How would the levels change in case (b) if 13.6 cm of water Ganmiscible with mercury) are poured into the right limb of the manometer 7 (Ignore the small change in the volume of the gas).

 

10.23 Two vessels have the same base area but different shapes. The first vessel takes twice the volume of water that the eecond veseel requires to fill upto a particular common height. Is the force exerted by the water on the base of the vessel the same in the two cases ? If so, why do the vessels filled with water to that same height give different readings on a weighing scale 7?

 

10.24 During blood tranafusion the needle is inserted in a vein where the gauge preasure is 2000 Pa. At what height must the blood container be placed ao that blood may juet enter the vein ? [Use the denaity of whole blood from Table 10.1].

 

10.25 In deriving Bernoulli's equation, we equated the work done on the fhuid in the tube to ita change in the potential and kinetic energy. (a) What is the largest average velocity of blood flow in an artery of diameter  2 x 10° m if the flow must remain laminar ? (b) Do the dissipative forces become more important as the fluid velocity

increases ? Diacusa qualitatively.

 

10.28 (a) What ts the largest average velocity of blood flow in an artery of radius 2x10“m if the flow must remain lanimar? (b} What ie the corresponding flow rate ? (Take viscosity of blood to be 2.084 x 10~ Pa a).

 

10.27 Aplane is in level flight at constant speed and each of its two wings has an area of 25 m*. If the speed of the air ia 180 km/h over the lower wing and 234 km/h over es PPer wing surface, determine the plane's mass. (Take air density to be 1 kg m™).

 

10.28 In Millikan’s oil drop experiment, what is the terminal speed of an uncharged drop of radius 2.0 x 10° m and denaity 1.2 x 10° kg m™. Take the viscosity of air at the temperature of the experiment to be 1.8 x 10° Pa a. How much is the viscous force on the drop at that speed ? Neglect bucyancy of the drop due to air.

 

10.29 Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside ? Surface tension of mercury at the temperature of the experiment is 0.465

Nm‘. Density of mercury = 13.6 x 10° kg m”,

 

10.30 Two narrow bores of diameters 3.0mm and 6.0 mm are joined together to form a U-tube open at both endpe. If the U-tube contains water, what ia the difference m ita levela in the two limbs of the tube ? Surface tenaion of water at the temperature of the experiment is 7.3 x 10? N m7". Take the angle of contact to be zero and denaity of water to be 1.0 x 10° kg m™ (g = Ofna,

Calculator/Computer - Based Problom

 

10.31 (a) It is known that denaity p of air decreases with height y as

p=pneu where 9, = 1.25 kg m° is the density at aca level, and y, is a constant. This denaity variation ie called the law of atmospheres. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions). Also assume

that the value of g remains constant.

 

(b) A large He balloon of volume 1425 m? is used to lift a payload of 400 kg. Assume that the balloon maintains constant radius as it rises. How high does it rise ?

[Take y, = 8000 m and p,, = 0.18 kg m*].

 

APPENDIX 10.1 : WHAT I8 BLOOD PRESSURE 7?

In evolutionary history there occurred a time when animals started spending a significant amount of time in the upright position. This placed a number of demands on the circulatory system. The venous system that returns blood from the lower extremities to the heart underwent changes. You will recall that veins are blood vessels through which blood returns to the heart. Humans and

animals such as the giraffe have adapted to the problem of moving blood upward against gravity.But animals such as snakes, rats and rabbits will die if held upwards, since the blood remains in the lower extremities and the venous system is unable to move it towarda the heart.

Figure 10.26 shows the average pressures observed in the arteries at various pointe in the human body.

Since viscous effects are small, we can use Bernoulli's equation, Eq. (10.13),

P+ = pe" +pagy = Constant to understand these pressure values. The kinetic energy term (p v*/2) can be ignored since the velocities in the three arteries are small (= 0.1 ms) and almost constant. Hence the gauge pressures at the brain P,,the heart P,, and the foot P,are related by P,= P+ pgh,=P,+pgh, (10.34)where p is the denaity of blood.

Typical values of the heights to the heart and the brain are h, = 1.3m and h, = 1.7m. Taking p= 1.06 x 10° kg m® we obtain that P, = 26.8 kPa (idlopascale) and P, = 9.3 kPa given that P, = 13.3 kPa.Thus the pressures in the lower and upper parts of the body are so different when a person is standing,but are almost equal when he ie lying down. As mentioned in the text the unite for pressure more commonly employed in medicine and physiology are torr and mm of Hg. 1 mm of Hg = 1 torr = 0.133 kPa.

Thue the average pressure at the heart ie P, = 13.3 kPa = 100 mm of Hg.

 

The human body is a marvel of nature. The veins in the lower extremities are equipped with valves,which open when blood flows towards the heart and close ff it tends to drain down. Also, blood is returned at least partially by the pumping action associated with breathing and by the flexing of the akeletal muscles during walking. This explains why a soldier who is required to stand at attention may faint because of

insufficient return of the blood to the heart. Once he is made to lie down, the pressures become equalized and he regains consciousness.

 

An instrument called the  sphygmomanometer usually measures the blood pressure of humane. It is a

fast, painless and non-invasive technique and gives the doctor a reliable idea about the patient's health.The measurement process is shown in Fig. 10.27. There are two reasons why the upper arm fa used. First,it fa at the eame level as the heart and measurements here give values close to that at the heart. Secondly,the upper arm contains a single bone and makes the artery there {called the brachial artery) easy to compress. We have all measured pulee rates by placing our fingers over the wrist. Each pulse takes a little lese than a second. During each pulse the pressure in the heart and the circulatory system goes through a

maximum as the blood is pumped by the heart (systolic pressure) and a minimum as the heart relaxes (diastolic pressure). The sphygmomanometer fa a device, which measures these extreme pressures. It works on the principle that bleod flow in the brachial (upper arm) artery can be made to go from

laminar to turbulent by suitable compression. Turbulent flow is  dissipative, and its sound can be

picked up on the stethoscope.

 

The gauge pressure in an air sack wrapped around the upper arm is measured using a manometer or a dial preseure gauge (Fig. 10.27). The preseure in the sack is first increased till the brachial artery is closed.The pressure in the sack is then slowly reduced while a stethoscope placed just below the sack is used to listen to noises arising in the brachial artery. When the pressure ie just below the systolic (peak)

preasure, the artery opens briefly. During this brief period, the blood velocity in the highly constricted

artery is high and turbulent and hence noisy. The resulting noise is heard as a tapping sound on the atethoscope. When the pressure in the sack is lowered further, the artery remaina open for a longer portion of the heart cycle. Nevertheless, it remains closed during the diastolic (minimum pressure)

phase of the heartheat. Thus the duration of the tapping sound is longer. When the pressure in the sack reaches the diastolic pressure the artery is

open during the entire heart cycle. The flow its however, still turbulent and noisy. But instead of a tapping sound we hear a steady, continuous roar on the stethoscope.

 

The blood pressure of a patient is presented as the ratio of  systolic/diastolic preasures. For a resting healthy adult it is typically 120/80 mm of Hg (120/80 torr). Pressures above 140/90 require medical

attention and advice. High blood pressures may sericualy damage the heart, kidney and other organs and

must be controlled.