Chapter 12 Thermodynamics

CHAPTER NO.12 THERMODYNAMICS

12.1 INTRODUCTION

In previous chapter we have studied thenmnal properties of Inatter. In this chapter we shall study laws that govern.

thermal energy. We shall study the processes where work is canverted into heat and vice versa. In winter, when we rub our palms together, we fee] warmer; here work done in rubbing produces the ‘heat’. Conversely, in a steam engine, the ‘heat’of the steam is used to do useful work in moving the pistons,

which in turn rotate the wheels of the train.

In physics, we need to deine the notions of heat,temperature, work, etc. more carefully. Historically, it took a

lang time to arrive at the proper concept of ‘heat’. Before the

modern picture, heat was regarded as a fine invisible fluid filling in the pores ofa substance. On contact between a hot body and a cold bedy, the fluid (called caloric) flowed from the colder to the hotter body ! This is similar to what happens when a horizontal pipe connects two tanks containing water

up to different heights. The flow continues until the kvels of water in the two tanks are the same. Likewise, in the ‘caloric’picture of heat, heat flows until the ‘caloric levels’ (i-e., the

temperatures) equalise.

In time, the picture of heat as a fluid was discarded in favour of the modern concept of heat as a form of energy. An

important experiment in this connection was due to Benjamin Thomson {also known as Count Rumford) in 1798. He obseryed that boring of a brass cannon generated a lot of heat, indeed enough to boil water. More significantly, the amount of heat produced depended on the work done {by the horses employed for turning the drill) but not on the sharpness of the drill. In the caloric picture, 4 sharper drill would scoop out more heat fluid from the pores; but this was not observed. A most natural explanation of the observations was that heat was a form of enengy and the experiment demonstrated conversion of energy from one form to another—irom work to heat.

Thermodynamics is the branch of physics that deals with the concepts of heat and temperature and the inter-conversion of heat and other forms of energy. Thermodynamics is a macroscopic

science. [t deals with bulk systems and does not go into the molecular constitution of matter. In fact, its concepts and laws were formulated in the

nineteenth century before the molecular picture of matter was finnly established. Thermodynamic description involves relatively few macroscopic

variables of the system, which are suggested by common sense and can be usually measured directly. A microscopic description of a gaa, for example, would involve specifying the co-ordinates

and velocities of the huge number of molecules constituting the gas. The description in kinetic theory of gases is not so detailed but it does hivolve

molecular distribution of velocities.

Thermodynamic description ofa gas, on the other hand, avoids the molecular description altogether.Instead, the state of a gas in thermodynamics is

specified by macroscopic variables such as pressure, vohume, temperature, mass and composition that are felt by our sense perceptions and are measurable*.

The distinction between mechanics and

thermodynamics is worth bearing in mind. In mechantks, our interest is in the motion of particles or bodies under the action of forces and torques.Thermodynamics is not concerned with the motion of the system as a whole. It is concerned with the internal macroscopic state of the body.When a bullet is fired from a gum, what changes

is the mechanical state of the bullet (its kinetic energy, in particular}, not its temperature. When the bullet pierces a wood and stops, the kinetic energy of the bullet gets converted into heat,

changing the termperature of the bullet and the surrounding Iayers of wood. Temperature is Telated to the energy of the internal (disordered)motion of the bullet, not to the motion of the bullet

as a whole.

12.2 THERMAL EQUILIBRIUM

Equilibrium in mechanics means that the net extemal force and torque on a system are zero.The term ‘equilibriuun’ in thenmodynaniiks appears ina different context : we say the state ofa system

is an equilibrium state if the macroscopic variables that characterise the system do not change in time. For example, a gas tnside a closed

rigid container, completely insulated from its surroundings, with fixed values of pressure,volume, temperature, mass and composttion that do not change with time, is in a state of thermodynamic equilibrium.

In general, whether or not a system is ina state of equilibrium depends on the surroundings and the nature of the wall that separates the system from the surroundings. Consider two gases Aand

B occupying two different containers. We know experimentally that pressure and volume of a given maas of gas can be chosen to be its two independent variables. Let the pressure and

volume of the gases be {P, Vv, and (P,, V,)respectively. Suppose first that the two systems are put in proximity but are separated by an adiabatic wall — an insulating wall (can be movable} that does not allow flow of energy (heat)

from one to another. The systems are insilated from the rest of the surroundings also by similar adiabatic walls. The situation {s shown

schematically in Fig. 12.1 {a). In this case, it is found that any possible pair of vahies (P,, V,) will be in equilfbriim with any poasible pafr of valies (P,, V,,}. Next, suppose that the adiabatic wall is replaced by 4 diathermic wall —a conducting wall

that allows enerpy flow (heat) fram one to another.It is then found that the macroscopic variables of the systems A and Bchange spontaneously until

both the syatems attatn equittbrium states. After that there is no change in their states. The situation is shown in Fig. 12.1(b). The pressure and vohume variables of the two gases change to

(P,‘, V,) and (P,’, V,’) such that the new states of A and Bare in equilfprtum with each other**.There is no more energy flow from one to another.

We then say that the system A is in thermal equilibrium with the system B.

What characterises the sttuation of thermal equilibrium between two systems ? You can guess the answer from your experience. In thermal equilibrium, the temperatures of the two systems

are equal. We shall see how does one arrive at the concept of temperature in thermodynamics?The Zeroth law of thermodynamics provides the clue.

12.3 ZEROTH LAW OF THERMODYNAMICS

Imagine two systems A and B, separated by an adiabatic wall, wile each is in contact with a third system C, via a conducting wall [Fig. 12.2{a)]. The

states of the systems (Le., their macroscopic variables) will change wntil both A and Bcome to thermal equilibrium with C. After this is achieved,suppose that the adiabatic wall between Aand B

is replaced by a conducting wall and Cis insulated from Aand Bby an adiabatic wall [Fig.12.2(b)]. It is found that the states of A and B change no further Le. they are found toe be in thermal

equilibrium with each other. This observation forms the basis of the Zeroth Law of Thermodynamics, which states that ‘two systems in thermal equilibrium with a third system separately are in thermal equilibrium

with each other’. RH. Fowler formulated this law in 1931 long after the first and second Laws of thermodynamics were stated and so numbered.

The Zeroth Law clearly suggests that when two systems A and B, are in thermal equilibrium,there must be a physical quantity that has the same value for both. This thermodynamic variable whose value is equal for two systems in

thermal equilibrium is called temperature (T).Thus, if A and B are separately in equilibrium with C, T, =Te and Tz = Te. This implies that

T, = Ty 1.e. the systems A and B are also in thermal equilibrium.

‘We have arrived at the concept of temperature formally via the Zeroth Law. The next question is: how to assign numerical values to temperatures of different bodies? In other words,

how do we construct a scale of temperature ?Thermometry deals with this basic question to which we turn in the next section.

12.4 HEAT, INTERNAL ENERGY AND WORK

The Zeroth Law of Thermodynamics led us to the concept of temperature that agrees with our commonsense notion. Temperature is a marker of the ‘hotness’ of a body. It determines the direction of flow of heat when two bodies are

placed in thermal contact. Heat flows from the body at a higher temperature to the one at lower temperature. The flow stops when the temperatures equalise; the two bodies are then in thermal equilibrium. We saw in some detail

how to construct temperature scales to assign temperatures to different bodies. We now describe the concepts of heat and other relevant quantities ke internal energy and work.

The concept of internal energy of a syatem is not difficult to understand, We know that every bulk system consists of a large number of molecules. Internal energy is amply the sum of the kinetic energies and potential enerpies of

these molecules. We remarked earler that in thermodynamics, the kinetic energy of the system, as a whole, is not relevant. Internal energy is thus, the sum of molecular kinetic and potential energies in the frame of reference Telative to which the centre of mass of the system

is at rest. Thus, it includes only the (disordered)energy associated with the random motion of molecules of the system. We denote the internal

energy of a system by U.

Though we have invoked the molecular

picture to understand the meaning of internal energy, as far as thermodynamics is concerned,Uis stmply a macroscopic variable of the system.

The important thing about internal energy is that it depends only on the state of the system,not on how that state was achieved. Internal energy U of a system is an example of a thermodynamic ‘state variable’ — its value depends only on the given state of the system.not on history Le. not on the ‘path’ taken to arrive at that state. Thus, the internal energy ofa given

mass of gas depends on its state described by specific values of pressure, volume and temperature. It does not depend on how this state of the gas came about Pressure, volume,

temperature, and internal energy are

thermodynamic state variables of the system (gas) (see section 12.7). if we neglect the small intermolecular forces in a gas, the internal energy of a gas is just the sum of kinetic energies

associated with various random motions of its molecules. We will see tn the next chapter that in a gas this motion is not only translational (i.e. motion from one point to another in the

volume of the container); it alsc includes rotational and vibrational motion of the molecules (Fig. 12.3).

What are the ways of changing internal

energy of a system ? Consider again, for

simplicity, the system to be a certain mass of gas contained in a cylinder with a movable piston as shown in Fig. 12.4. Experience shows there are two ways of changing the state of the gas (and hence its internal energy). One way is

to put the cylinder in contact with a body at a higher temperature than that of the gas. The temperature difference will cause a flow of energy (heat) from the hotter body to the gas,thus fucreasing the internal energy of the gas.The other way is to push the piston down t.e. to do work on the system, which again results in increasing the internal energy of the gas. Of

course, both these things could happen in the reverse direction. With surroundings at a lower temperature, heat would flow from the gas to

the surroundings. Likewise, the gas coukl push the piston up and do work on the surroundings.In short, heat and work are two different modes of altering the state ofa thermodynamic system

and changing its internal energy.

The notion of heat should be carefully

distinguished from the notion of internal energy.Heat is certainly energy, but it is the energy in

transit. This is not just a play of words. The distinction is of basic significance. The state of a thermodynamic system is characterised by its internal energy, not heat. A statement like ‘a gas in a given state has a certain amount of heat’ is as meaningless as the statement that

‘a gas in a given state has a certain amount of work’. In contrast, ‘a gas in a given state has a certain amount of internal energy’ is a perfectly meaningful statement. Stmilarly, the

Statements ‘a certain amount of heat is

supplied to the system’ or ‘a certain amount of work was done by the system’ are perfectly meaningful.

To summarise, heat and work in

thermodynamics are not state variables. They are modes of energy transfer to a system resiuting in change in ite internal energy,which, as already mentioned, is a state variable.In ordinary language, we often confuse heat with internal energy. The distinction between them is sometimes ignored in elementary physics books. For proper understanding of thermodynamics, however, the distinction s crucial.

12.6 FIRST LAW OF THERMODYNAMICS

We have seen that the internal energy U of a system can change through two modes of energy transfer : heat and work. Let

AQ = Heat supplied to the system by the

surroundings AW = Work done by the system on the surroundings AU = Change in internal energy of the system

The general principle of conservation of

energy then implies that AQ = AU+AW (12.1) i.e. the energy (AG) supplied to the syatem goes in partly to increase the internal energy of the system (AU) and the rest in work on the environment (AW). Equation (12.1) is known as

the First Law of Thermodynamics. It is simply the general law of conservation of energy applied to any system in which the energy transfer from or to the surroundings is taken into account.

Let us put Eq. (12.1) in the alternative form AQ - AW =AU (12.2)

Now, the system may go from an initial state to the final state in a number of ways. For example, to change the state of a gas from (P,. V,) to (P,, V). we can firat change the volume of the gas from V, to V,, keeping its pressure constant 1.c. we can first go the state

(P,. V,) and then change the preasure of the gas from P, to P,, keeping volume constant, to take the gas to (P,. V,). Alternatively, we can first keep the volume constant and then keep

the pressure constant. Since U is a atate variable, AU depends only on the initial and final states and not on the path taken by the gas to go from one to the other. However, AQ and AW will, in general, depend on the path taken to go from the initia] to final states. From

the Firat Law of Thermodynamics, Eq. (12.2).it is clear that the combination AG - AW, is however, path independent. This shows that tifa system is taken through a process in which AU = 0 (for example, isothermal expansion of

an ideal gas, see section 12.8),

AQ =AW 1e., heat supplied to the system is used up entirely by the system in doing work on the environment.

If the system is a gas in a cylinder with a movable piston, the gas in moving the piston doea work. Since force is preasure times area,and area times diaplacement is volume, work done by the system against a constant pressure

Pis

AW =PAV

where AV is the change in volume of the gas.Thus, for this case, Eq. (12.1) gives AQ = AU+ PAV (12.3)

As an application of Eq. (12.3), consider the change in internal energy for 1 ¢ of water when we go from its liquid to vapour phase. The measured latent heat of water is 2256 J/g. i.e.,

for 1 g of water AQ = 2256 J. At atmospheric pressure, 1 g of water has a volume | cm? in liquid phase and 1671 cm? in vapour phase.Therefore,AW=P(V,-V,) = 1.013 x10° x(1670)x10° =169.2J Equation (12.3) then gives AU= 2256 - 169.2 = 2086.87 We see that most of the heat goes to increase the internal energy of water in transition from the liquid to the vapour phase.

12.6 SPECIFIC HEAT CAPACITY

Suppose an amount of heat AQ supplied to a substance changes its temperature from T to T+ AT. We define heat capacity of a substance (2ee Chapter 11) to be

249 Saar (12.4)

We expect AQ and, therefore, heat capacity S to be proportional to the mass of the substance.Further, it could also depend on the temperature, 1.¢., a different amount of heat may be needed for a untt rise in temperature at

different temperatures. To define a constant characteristic of the substance and independent of its amount, we divide S by the mass of the substance m in kg:

— 8 _ f1\ag

s= a= (— Ke (12.5)

8 is known as the specific heat capacity of the substance. It depends on the nature of the substance and its temperature. The unit of specific heat capacity is Jkg?} K1.If the amount of substance is specified in terms of moles p (instead of mass min kg), we can define heat capacity per mole of the

substance by S 1aAQ9 Cc WAT (12.6)

C is known as molar specific heat capacity of the substance. Like s, C is independent of the amount of substance. C depends on the nature of the substance, its temperature and the

conditions under which heat is supplied. The unit of C is J mol" K". As we shall see later (in connection with spectfic heat capacity of gases),additional conditions may be needed to define

C or s. The idea in defining C is that simple predictions can be made in regard to molar specific heat capacities.

Table 12.1 lists measured specific and molar heat capacities of solids at atmospheric pressure and ordinary room temperature.We will see in Chapter 13 that predictions of specific heats of gases generally agree with experiment. We can use the same law of equipartition of energy that we use there to

predict molar specific heat capacities of solids.Consider a solid of N atoms, each vibrating about its mean position. An oscillator in one dimension has average energy of 2 x % kT = k,T. In three dimensions, the average energy

is 3 k,T. Fora mole ofa solid, the total energy is U =3k,T xN, =3RT

Now, at constant pressure, AQ = AU + PAV=

AU, since for a solid AV 1s negligible. Therefore,

c AQ _AU gn 12 AT AT 02.7)

Table 12.1 Specific and molar heat capacities of some solids at room

temperature and atmospheric

pressure

As Table 12.1 shows, the experimentally

Measured values which generally agrees with predicted value 3R at ordinary temperatures.

(Carbon is an exception.) The agreement is imown to break down at low temperatures.Specific heat capactty of water The old unit of heat was calorie. One calorie was earlier defined to be the amount of heat required to raise the temperature of 1g of water

by 1°C. With more precise measurements, tt was found that the specific heat of water varies slightly with temperature. Figure 12.5 showa this variation in the temperature range 0 to 100°C.

For a precise definition of calorie, it was,therefore, necessary to specify the unit temperature interval. One calorie is defined to be the amount of heat required to raise the temperature of 1g of water from 14.5 °C to 15.5 °C. Since heat is just a form of energy.it 1a preferable to use the unit joule, J.

In SI units, the specific heat capacity of water is 4186 J kg! K' i.e. 4.186 J g! K". The so called mechanical equtvalent of heat defined as the amount of work needed to produce 1 cal of heat is in fact just a conversion factor

between two different units of energy : calorie to joule. Since in SI units, we use the unit joule for heat, work or any other form of energy, the term mechanical equivalent is now

superfluous and need not be used.

As already remarked, the specific heat

capacity depends on the procesa or the

conditions under which heat capacity transfer takes place. For gases, for example, we can define two specific heats : specific heat capacity at constant volume and specific heat capacity at constant pressure. For an

ideal gas, we have a simple relation.

C,- C,=R (12.8)where C, and C, are molar specific heat capacities of an ideal gas at constant pressure and vohame respectively and R is the universal

gas constant. To prove the relation, we begin with Eq. (12.3) for 1 mole of the gas :AQ =AU+ PAV If AQ is absorbed at constant volume, AV =0 «-(22) ~(a4) (28)

& ( aT}, Var}, Var (12.9)

where the subscript v is dropped in the last step, since U of an ideal gas depends only on temperature. (The subscript denotes the quantity kept fixed.) If, on the other hand, AQ

is absorbed at conatant pressure,

Ty (AQ) — (AU AV )

c= (Rl (Gel rar] azo

The subscript p can be dropped from the

first term since U of an ideal gas depends only on T. Now, for a mole of an ideal gas PV=RT which gives 1 (AV

° (7), =k (12.11) Equations (12.9) to (12.11) give the desired Telation, Eq. (12.8).

12.7 THERMODYNAMIC STATE VARIABLES

AND EQUATION OF STATE

Every equilibrium state of a thermodynamic system is completely described by specific values of some macroscopic variables, also called state variables. For example, an equilibrium state of a gas is completely specified by the values of pressure, volume,

temperature, and mass (and composition if there is a mixture of gases). A thermodynamic syatem is not always in equilibrium. For example,a gas allowed to expand freely against vacuum

is not an equilibrium state [Fig. 12.6{a}]. During the rapid expansion, preasure of the gaa may not be untform throughout. Similarly, a mixture

of gases undergoing an explosive chemical reaction (e.g. a mixture of petrol vapour and air when ignited by a spark) is not an equilibrium state; again its temperature and pressure are not wniform [Fig. 12.6(b)].Eventually, the gaa attains a uniform temperature and pressure and comes to thermal and mechanical equilibrium with its

surroundings.

In short, thermodynamic state variables

describe equilibrium states of systems. The various state variables are not necessarily independent. The connection between the state variables is called the equation of state. For example, for an ideal gas, the equation of state

is the ideal gas relation

PV=pRT

For a fixed amount of the gas i.e. given p, there are thus, only two independent variables, say P and V or Tand V. The pressure-volume curve for a fixed temperature is called an isotherm.

Real gases may have more complicated

equations of state.

The thermodynamic state variables are of two kinds: extensive and intensive. Extensive variables indicate the ‘size’ of the system.Intensive variables such as pressure and temperature do not. To decide which variable is extensive and which intensive, think of a relevant system in equilibrium, and imagine that

it 1s divided into two equal parts. The variables that remain unchanged for each part are intensive. The variables whose values get halved in each part are extensive. It is easily seen, for

example, that internal energy U, volume V, total mass M are extensive variables. Pressure P,temperature T, and density p are intensive variables. It is a good practice to check the consistency of thermodynamic equations using this clasatfication of variables. For example, in the equation AQ=AU+ PAV quantities on both sides are extensive®. (Theproduct of an intensive variable like P and an extensive quantity AV is extensive.)

12.8 THERMODYNAMIC PROCESSES

12.8.1 Quasi-static process

Consider a gas in thermal and mechanical

equilibrium with its surroundings. The pressure of the gas in that case equals the external pressure and its temperature is the same as that of its surroundings. Suppose that the external pressure is suddenly reduced (say by lifting the weight on the movable piston in the container). The piston will accelerate outward.During the process, the gas passes through states that are not equilfbriium states. The non-

equilibrium states do not have well-defined pressure and temperature. In the same way, if a finite temperature difference exists between the gas and its surroundings, there will be a rapid exchange of heat during which the gas

will pass through non-equilibrium states. In due course, the gas will settle to an equilibrium state with well-defined temperature and

presaure equal to those of the surroundings. The free expansion ofa gas in vacuum and a mixture of gasea undergoing an explosive chemical

reaction, mentioned in section 12.7 are also examples where the system goes through non-equilibrium states.

Non-equilibrium states of a system are difficult to deal with. It is, therefore, convenient to imagine an idealised process in which at every

stage the system is an equilibrium atate. Such a process is, in principle, infinitely slow-hence the name quasi-static (meaning nearly static). The

system changes its variables (P, T, V) so slowly that {t remains in thermal and mechanical equilibrium with fis aurroundings throughout.In a quasi-static process, at every stage, the

difference in the pressure of the system and the external pressure is infinitesimally small. The same is true of the temperature difference

between the syatem and its surroundings. To take a gas from the state (P, T) to another state (P’. T’)} via a quasi-static process, we change the external pressure by a very small amount,

allow the system to equalise its pressure with that of the surroundings and continue the process infinitely slowly until the system achieves the pressure P’. Similarly, to change

the temperature, we introduce an infinitesimal temperature difference between the system and the surrounding reservoirs and by choosing reservoirs of progressively different temperatures

T to T’, the system achieves the temperature T’.A quasi-static process is obviously a hypothetical construct. In practice, processes that are sufficiently slow and do not involve

accelerated motion of the piston, large

temperature gradient, etc. are reasonably approximation to an ideal quasi-static proceas.We shall from now on deal with quasi-static processes only, except when stated otherwise.

A process in which the temperature of the system is kept fixed throughout is called an isothermal process. The expansion ofa gas in a metallic cylinder placed in a large reservoir of

fixed temperature is an example of an isothermal process. {Heat transferred from the reservoir to the system does not materially affect the temperature of the reservoir, becanse of its very

large heat capacity.) In isobaric processes the pressure is constant while in isochoric processes the volume is constant. Finally, if the system is insulated from the surroundings

and no heat flows between the system and the surroundings, the process is adiabatic. The definitions of these special processes are summarised in Table. 12.2 Table 13.2 Some special thermodynamic

processes

We now consider these processes in some detail :Isothermal process For an isothermal process (T fixed), the ideal gas equation gives PV = constant

Le., pressure ofa given mass of gas varies inversely as its volume. This is nothing but Boyle’s Law.

Suppose an ideal gas goes isothermally (at temperature T) from its initial state (P,. V,) to the final state (P,. V,). At any intermediate stage with pressure P and volume change from V to

V+ AV (AV small)AW = PAV Taking (AV — 0) and summing the quantity AW over the entire process,oy We] Pdv V,, Vv.

2dv Vv, wee > = BERT ns (12.12)

where in the second step we have made use of the ideal gas equation PV =p) RT and taken the constants out of the integral. For an ideal gas,internal energy depends only on temperature.

Thus, there is no change in the internal energy of an ideal gas in an isothermal procesa. The First Law of Thermodynamics then implies that heat supplied to the gas equals the work done by the gas : Q = W. Note from Eq. (12.12) that

for V,> V,, W> 0; and for V,< V,, W<0. That is, in an isothermal expansion, the gas absorbs heat and doea work while in an isothermal compression, work is done on the gas by the environment and heat ts released.

Adiabatic process

In an adiabatic process, the system is insulated from the surroundings and heat absorbed or Teleased is zero. From Eq. (12.1), we see that work done by the gas results in decrease in its internal energy (and hence its temperature for

an ideal gas). We quote without proof (the result that you will learn in higher courses) that for an adiabatic proceas of an ideal gas.PV’ = const (12,13)where y is the ratio of specific heats (ordinary or molar) at constant pressure and at constant volume.

7 Cy

Thus if an ideal gas undergoes a change in its state adiabatically from (P,, V,) to (P,, V.) :P vy =P, vy (12.14)

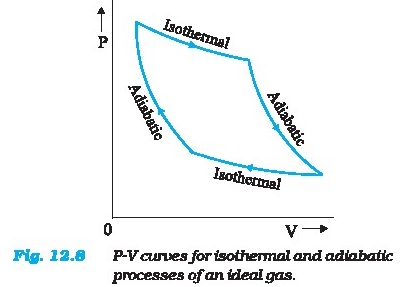
Figure 12.8 shows the P-V curvea of an ideal gas for two adiabatic processes connecting two isotherms.

We can calculate, aa before, the work done in an adiabatic change of an ideal gas from the state (P,, V,, T,) to the state (P,, V,, T,).OY We | PdV Y

V5 dv yor Vv;=constant x } —=constant x — Vv, Vi 1-¥ Vv,constant 1 1 From Eq. (12.34), the constant ts PV," or PV,"

w - J! PVy' JPl-y[ vs v7 _ BRC, - 7.)=[oylevs-PMJ-—~a = a216)

As expected, if work is done by the gas in an adiabatic process (W > 0}, from Eq. (12.16),T, <T,. On the other hand, if work is done on the gas (W < 0), we get T, > T, i.c., the temperature of the gas rises.

Isochoric process

In an isochoric process, Vis constant. No work is done on or by the gas. From Eq. (12.1), the heat absorbed by the gas goes entirely to change its internal energy and its temperature. The

change in temperature for a given amount of heat is determined by the specific heat of the gas at constant volume.

Isobaric process

In an isobaric process, P is fixed. Work done by the gas is W=PiV,-V) = HR(T,-T) (12.17)

Since temperature changes, so does internal energy. The heat absorbed goes partly to increase internal energy and partly to do work.The change in temperature for a given amount

of heat is determined by the specific heat of the gas at constant pressure.

Cyclic process

In a cyclic process, the system returns to its initial state. Since internal energy is a state variable, AU = 0 for a cyclic process. From Eq. (12.1), the total heat absorbed equals the work done by the system.

12.0 HEAT ENGINES

Heat engine is a device by which a system is made to undergo a cyclic process that results in conversion of heat to work.

(1) It consists of a working substance-the system. For example, a mixture of fuel vapour and air in a gasoline or diesel engine or steam in a steam engine are the working substances.

(2) The working substance goes through a cycle consisting of several processes. In some of these processes, it absorbs a total amount of heat Q, from an external reservoir at some high temperature T,,.

(3) In some other processes of the cycle, the working substance releases a total amount of heat Q, to an external reservoir at some lower temperature T,.

(4 The work done (W) by the system in a cycle is transferred to the environment via some arrangement (e.g. the working substance may be in a cylinder with a moving piston that transfers mechanical energy to the wheels of a vehicle via a shaft).

The basic features of a heat engine are

schematically represented in Fig. 12.9.

The cycle is repeated again and again to get useful work for some purpose. The discipline of thermodynamics has its roots in the study of heat engines. A basic question relates to the efficiency

of a heat engine. The efficiency (n) of a heat engine is defined by ow

Or (12.18)where Q, is the heat input i.ec., the heat absorbed by the system in one complete cycle and W is the work done on the environment in a cycle. Ina cycle, a certain amount of heat (Q,}

may also be rejected to the environment. Then,according to the First Law of Thermodynamics,over one complete cycle,

w=9,-9, (12.19)

i.e.,

=|-22

7=1 Q1 (12.20)

For 9, = 0, 1 = 1, Le., the engine will have 100% efficiency in converting heat into work.Note that the Firat Law of Thermodynamics tLe.,the energy conservation law does not rule out

such an engine. But experience shows that such an ideal engine with 7 = 1 is never possible,even if we can eliminate various kinda of loases associated with actual heat engines. It turns out that there is a fundamental limit on the

efficiency of a heat engine set by an independent principle of nature, called the Second Law of Thermodynamics (section 12.11).

The mechanism of conversion of heat into

work varies for different heat engines. Basically,there are two ways : the system (say a gas ora mixture of gases) ia heated by an external furnace, as in a steam engine; or ft is heated

internally by an exothermic chemical reaction as in an internal combustion engine. The various steps involved in a cycle also differ from one engine to another.

12.10 REFRIGERATORS AND HEAT PUMPS

A refrigerator is the reverse of a heat engine.Here the working substance extracts heat Q,from the cold reservoir at temperature T,, some external work W is done on it and heat 9, is released to the hot reservoir at temperature T,

(Fig. 12.10).

Pioneers of Thermodynamics Lond Kelvin (William Thomson) (1824-1907), born in Belfast, Ireland, is . among the forcmost British scientists of the nineteenth century. Thomson a< j played a key role in the development of the law of conservation of energy ans Suggested by the work of James Joule {1518-1889}, Julius Mayer (1814 f Rd 1878) and Hermann Helmholtz (1821-1894), He collaborated with Joule 7 A rr on the so-called Joule-Thomaon effect : cooling of a gas when it expands : a ; inte vacuum. He introduced the notion of the absolute zero of temperature—_ VY and propoeed the abeolute temperuture acale, now called the Kelvin ecale " * tn his honour. From the work of Sadi Carnot (1796-1832), Thomson arrived at a form of the Second Law of Thermodynamics. Thomson was a versatile physiciet, with notable contributions ta clectromagnetic theory and hydrodynamics.

0 Radolf Claustus (1822-1888), born in Poland, is generally regarded as

the discoverer of the Second Law of Thermodynamics. Based an the work

of Camot and Thomson, Clauaiue arrived at the important notion of entropy

that led bim to a fundamental version of the Second Law of Thermodynamics that states that the entropy of an isolated system can never decrease. Clausins also worked on the kinetic theory of gases and obtained the firat reliable estimates of molecular size, speed, mean free path, ete.

A heat pump is the same as a refrigerator.What term we use depends on the purpose of the device. If the purpose is to cool a portion of

apace, like the inside of a chamber, and higher temperature reservoir is surrounding, we call the device a refrigerator; if the idea is to pump

heat into a portion of space (the room in a building when the outside environment is cold),the device is called a heat pump.

In a refrigerator the working substance

(usually, {n gaseons form) goes through the following steps : (a) sudden expansion of the gas from high to low pressure which cools it and

converts it into a vapour-liquid mixture, (b)absorption by the cold fluid of heat from the region to be cooled converting it into vapour, (c)heating up of the vapour due to external work

done on the system, and (d) release of heat by the vapour to the surroundings, bringing it to the initial state and completing the cycle.

The coefficient of performance (a) of a

refrigerator is given by 92 a= (12.21)

where Q, is the heat extracted from the cold reservoir and W is the work done on the system-the refrigerant. (a for heat pump is defined as 9, /W) Note that while 7 by definition can never exceed 1, a can be greater than 1.By energy conservation, the heat released to the

hot reservoir is 9,=W+Q,fe. & “90 (12.22)In a heat engine, heat cannot be fully converted to work; likewise a refrigerator cannot work without some external work done on the syatem, i.e., the coefficient of performance in Eq.

(12.21) cannot be infinite.

12.11 SECOND LAW OF THERMODYNAMICS

The First Law of Thermodynamics is the principle of conservation of energy. Common experience shows that there are many conceivable processes that are perfectly allowed by the First

Law and yet are never observed. For example,nohody has ever seen a book lying on a table jumping to a height by ftself. But such a thing would be possible if the principle of conservation of energy were the only restriction. The table could cool spontaneously, converting some of its

internal energy into an equal amount of

mechanical energy of the book, which would then hop to a height with potential energy equal to the mechanical energy it acquired. But this never happens. Clearly, same additional basic

principle of nature forbids the above, even though it satisfies the energy conservation principle. This principle, which disaflows many phenomena consistent with the First Law of

Thermodynamics is known as the Second Law of Thermodynamics.

The Second Law of Thermodynamics gives a

fundamental limitation to the efficiency of a heat engine and the co-efficient of performance of a refrigerator. In simple terms, it says that efficiency of a heat engine can never be unity.According to Eq. (12.20). this implies that heat

released to the cold reservoir can never be made zero. For a refrigerator, the Second Law says that the co-efficient of performance can never be infintte. According to Eq. (12.21), this implics

that external work (W) can never be zero. The following two statements, one due to Kelvin and Planck denying the possibility of a perfect heat

engine, and another due to Clausius denying the possibility of a perfect refrigerator or heat pump, are a concise summary of these observations.

Second Law of Thermodynamics Kelvin-Planck statement.No process is possible whose sole result is the absorption of heat from a reservoir and the

complete conversion of the heat into work.Clausius statement No process is possible whoae sole result is the

transfer of heat from a colder object to a hotter object.It can be proved that the two statements above are completely equivalent.

123.12 REVERSIBLE AND IRREVERSIBLE PROCESSES

Imagine some process in which a thermodynamic system goes from an initial state 1 to a final state jf: During the process the system absorbs

heat 9 from the surroundings and performs work W on it. Can we reverse this process and bring both the system and surroundings to their initial states with no other effect anywhere ?

Experience suggests that for most processes in nature this is not possible. The spontaneous processes of nature are irreversible. Several

exampks can be cited. The base of a vesse] on an oven is hotter than its other parts. When the vessel is removed, heat is transferred from the base to the other parts, bringing the vessel

to a uniform temperature (which in due course cools to the temperature of the surroundings).The process cannot be reversed; a part of the vessel will not get cooler spontaneously and warm up the base. It will violate the Second Law

of Thermodynamics, if it did. The free expansion of a gas is irreversible. The combustion reaction of a mixture of petrol and air ignited by 4 spark

cannot be reversed. Cooking gas leaking from a gas cylinder in the kitchen diffuses to the entire room. The diffusion proceas will not spontancously reverse and bring the gas back

to the cylinder. The stirring of a Hquid in thermal contact with a reservoir will convert the work done into heat, increasing the internal energy of the reservoir. The process cannot be reversed exactly; otherwise it would amount to conversion of heat entirely into work, violating the Second

Law of Thermodynamics. Irreversibility is a rule rather an exception in nature.

Irreversibility arises mainly from two causes:one, many processes (like a free expansion, or an explosive chemical reaction) take the aystem to non-equilibrium states; two, mast processes

involve friction, viscosity and other dissipative effects (e.g., a moving body coming to a stop and losing its mechanical energy as heat to the floor

and the body, a rotating blade in a Hquid coming to a stop due to viscosity and losing its mechanical energy with corresponding gain in the internal energy of the liquid). Since

disstpative effects are present everywhere and can be minimised but not fully eliminated, most processes that we deal with are irreversible.

Athermodynamic process (state !— state f)is reversible if the process can be turned back such that both the system and the surroundings return to their original states, with no other

change anywhere else tn the universe. From the preceding discussion, a reversible process is an idealised notion. A process is reversible only if

itis quasi-static (system in equilibrium with the surroundings at every stage) and there are no dissipative effects. For example, a quasi-static isothermal expansion of an ideal gas in a

cylinder fitted with a frictionless movable piston is a reveraible process.

Why is reversibility such a basic concept in thermodynamics 7? As we have seen, one of the concerns of thermodynamics is the efficiency

with which heat can be converted into work.The Second Law of Thermodynamics rules cut the possibility of a perfect heat engine with 100% efficiency, But what is the highest efficiency

possible for a heat engine working between two reservoirs at temperatures T, and T,? It turns out that a heat engine based on idealised reversible processes achieves the highest

efficiency possible. All other engines involving irreversibility in any way (as would be the case for practical engines) have lower than this Imiting efficiency.

12.13 CARNOT ENGINE

Suppose we have a hot reservotr at temperature T, and a coki reservoir at temperature T,. What is the maxtnum efficiency possible for a heat

engine operating between the two reservoirs and what cycle of processes should be adopted to achieve the maximum efficiency ? Sadi Carnot,a French engineer, first considered this question

in 1824. Interestingly, Carnot arrived at the correct answer, even though the basic concepts of heat and thermodynamics had yet ta he firmly

established.

We expect the ideal engine operating between two temperatures to be a reversible engine.lrreversibility is associated with dissipative effects, as remarked in the preceding section,

and lowers efficiency. A process is reversible if it ia quaai-static and non-disaipative. We have seen that a process is not quasi-static if it

involves finite temperature difference between the system and the reservoir. This implies that in a reversible heat engine operating between two temperatures, heat should be absorbed

(from the het reservoir) isothermally and released (to the cold reservoir) isothermally. We thus have identified two steps of the reversible heat engine : isothermal process at temperature

T, absorbing heat 9, from the hot reservoir, and another isothermal process at temperature T,releasing heat Q, to the cold reservoir. To complete a cycle, we need to take the system from temperature T, to T, and then back from

temperature T, to T,. Which processes should we employ for this purpose that are reversible?

A little reflection shows that we can only adopt reversible adiabatic processes for these purposes, which involve no heat flow from any

reservoir. If we employ any other proceas that is not adiabatic, say an isochoric process, to take the system from one temperature to ancther, we

shall need a series of reservoirs in the

temperature range T, to T, to ensure that at cach stage the process is quasi-static. (Remember again that for a process to be quasi-static and

reversible, there should be no finite temperature difference between the system and the reservoir.)But we are considering a reversible engine that

operates between only two temperatures. Thus adiabatic processes must bring about the temperature change in the system from T, to T,and T, to T, in this engine.

A reversible heat engine operating between two temperatures is called a Carnot engine. We have just argued that such an engine must have the following sequence of steps constituting one

cycle, called the Carnot cycle, shown in Fig. 12.11. We have taken the working substance of the Carnot engine to be an ideal gus.

(a) Step 1 > 2 Isothermal expansion of the gas taking its state from (P., V,, T,) to (P,, V,, T).The heat absorbed by the gas (Q,) from the reservoir at temperature T, is given by Eq, (12.12). This is also the work done (W, ,.)

by the gas on the environment.1,Ws = 9, =HRT, In (x4) (12.23)(b) Step2-—3 Adiabatic expanaton of the gas from (P,, V,. T;) to (P,, Vy. T;)Work done by the gas, using Eq. (12.16), is wy HRD -T.|

Ws a (12.24)(c) Step3— 4 Isothermal compression of the gas from (P,, V,, T,) to (P,, V,, T,).Heat released (Q,) by the gas to the reservoir at temperature T, is given by Eq. (12.12). This

is also the work done (W, _, ,) on the gas by the environment.. ly,Ws.4 = Q = wRTeAn| (12.25). a (@) Step4—1 Adtabatic compression of the gas from (P, V,, T,) to (P,.V,. T).Work done on the gaa, [using Eq.(12.16)], is (T, -T;)

Wi. =uR “= =e | (12.26)From Eqs. (12.23) to (12.26) total work done by the gas in one complete cycle is W=W, 2 + Wo3-Ws 44-Wasi Vp Ws = RT, In (i) —- HRT, im( 7) (12.27)The efficiency 7 of the Carnot engine is Me g, 9,. n( Ze _ Ty V, ?

=! -( 2 nas (12.28)nl Now since step 2 —> 3 is an adiabatic process,, gel vol

T, Vy =T) Vy , Gen 2 ({hLe. V, = ( T, | (12.29)Similarly, since step 4 — 1 is an adiabatic process T, Vy m =f, v

‘ ylfyel le. = & (12.80)e. Vv; 7, | .

From Eqs. (12.29) and (12.30), ‘Va _V;

Tv (12.31)Using Eq. (12.31) in Eq. (12.29), we get . r nel “"7, (Camot engine) (12.32)We have already seen that a Carnot engine is a reveraible engine. Indeed ft is the only reversible engine possible that works between two reservoirs at different temperatures. Each step of the Carnot cycle given in Fig. 12.11 can be reversed. This will amount to taking heat 9,from the cold reservoir at T,, doing work W on

the system, and transferring heat Q, to the hot Teservoir. This will be a reverafble refrigerator.

We next establish the important result

(sometimes called Carnot’s theorem) that

(a) working between two given temperatures T,and T, of the hot and cold reservoirs respectively,no engine can have efficiency more than that of

the Carnot engine and {b) the efficiency of the Carnot engine is independent of the nature of the working substance.

To prove the result (a), imagine a reversible (Carnot) engine R and an irreversible engine I working between the same source (hot reservotr)and sink (cold reservoir}. Let us couple the

engines, I and R, in such a way so that I acts like a heat engine and R acts as a refrigerator.Let I absorb heat Q, from the source, deliver work W’ and release the heat 9,- W to the sink.We arrange so that R returns the same heat 9,to the source, taking heat O, from the sink and

reauiring work W = O. = OQ. to be done on tt.

Now suppose ny < 7, 1c. if R were to act

as an engine it would give less work output than that of lic. W< W’ fora given 9,. With R acting like a refrigerator, this would mean

9,= 9.-W> QO, -W’. Thus on the whole,

the coupled I-R system extracts heat

reservoir and delivers the same amount of work in one cycle, without any change in the source or anywhere else. This is clearty against the Kelvin-Planck statement of the Second Law of

Themnodynamics. Hence the assertion 7, > ti,is wrong. No engine can have efficiency greater than that of the Carnot engine. A similar argument can be constructed to show that a reversible engine with one particular substance

cannot be more efficient than the one using another substance. The maximum efficiency of a Carnot engine given by Eq. (12.32) is independent of the nature of the system Perfonning the Carnot cycle of operations. Thus ‘Wwe are justified in using an ideal gas as a system in the calculation of efficiency n of a Carnot engine. The ideal gas has a simple equation of state, which allows us to readily calculate n, but the final result for n, [Eq. (12.32)], is true for

any Carnot engine.

This final remark shows that in a Carnot

cycle,T; Baa (12.39)ia a universal relation tndependent of the nature

of the syatem. Here 9, and Q, are reapectively,the heat abaorbed and released iaothermally (from the hot and to the cold reservoirs) in a Carnot engine. Equation (12.33), can, therefore,be used as a relation to define a truly universal thermodynamic temperature scale that ia independent of any particular properties of the

system used in the Carnot cycle. Ofcourse, for an ideal gas as a working substance, this universal temperature is the same as the ideal gas temperature introduced in section 12.11.

SUMMARY

1. The zeroth law of thermodynamics states that ‘two systems tn thermal equilfbram with a third system are in thermal equilibrium with each other. The Zeroth Law leads to the concept of temperature.

2. Internal energy of a system is the sum of kinetic energies and potential energies of the molecular constituents of the system. It does not inchide the over-all kinetic energy of the system. Heat and work are two modes of energy transfer to the system. Heat is the

energy tranefer ariaing due te temperature difference between the system and the surroundings, Work is energy transfer brought about by other means, such as moving the piston of a cylinder containing the gas, by raiaing or lowering some weight connected

to it.

3. The first law of thermodynamics is the general law of conservation of energy applied to any system in which energy tranafer from or to the surroundings (through heat and work} is taken into account. It statea that

4Q =AU + AW where AQ ia the heat supplied to the system, AW is the work done by the system and AU is the change in internal energy of the system.

4. The apecific heat capacity of a substance is defined by "1 AQ s=_>

m AT where m is the mass of the substance and AQ is the heat required to change ite temperature by AT. The molar spectfic heat capacity of a substance ta defined by cul Ag yeAT where jt is the number of moles of the substance. For a solid, the law of equipartition of energy gtvea C=3R which generally agrees with experiment at ordinary temperatures.Calorie is the old unit of heat. 1 calorie is the amount of heat required to raise the temperature of 1 g of water from 14.6 °C to 15.6 °C. lcal = 4.186 J.

5. For an ideal gas, the molar specific heat capacities at constant pressure and volume aatialy the relation c,-C, =R

where R is the universal gas constant.

6. Equilibrium states of a thermodynamic system are deacribed by state variables. The value of a state variable depends only on the particular state, not on the path used to arrive at that state. Examples of state variables are preaaure (P), volume (V), temperature (T), and mass (m)}. Heat and work are not state variables. An Equation of State (like

the ideal gas equation PV = jt RT) ia a relation connecting different state variables.

7. A quasi-static process is an infinitely slow procese such that the system remains in thermal and mechanical equilibrium with the surroundings throughout. In a quasi-static process, the pressure and temperature of the environment can differ from those of the system only infinitesimally.

8. In an isothermal expansion of an ideal gas from volume V, to V, at temperature T the heat absorbed (Q equals the work done (W) by the gas, each given by . vy Q=We= zpRT Vy

9. In an adiabatic process of an ideal gas Pv" = constant . C where y= C,

Work done by an ideal gas in an adiabatic change of state from (P,, V,, T,) to (P,, V,, T,)ia wetRG-T) 7-1

10. Heat engine is a device in which a system undergoes a cyclic process resulting in conversion of heat into work. If 9, 1s the heat absorbed from the source, Q, is the heat released to the sink, and the work output in one cycle is W, the efficiency 9 of the engine ia:no W 1. B 9; 9g:

11. Ina refrigerator or a heat pump, the system extracts heat Q, from the cold reservoir and releases Q, amount of heat to the hot reservotr, with work W done on the system. The co-efficient of performance of a refrigerator is given by Qe Q» C= W Q91-Q2

12. The second law of thermodynamics disallows aome processes conaistent with the First Law of Thermodynamics. It atates Keluin-Planck statement No process ia possible whose sole result is the absorption of heat from a reservoir and complete conversion of the heat into work.

Claustus sintement

No process is possible whose sole result ia the transfer of heat from a colder object to a hotter object.Put aimply, the Second Law implica that no heat engine can have efficiency y equal to

1 or no refrigerator can have co-efficient of performance o equal to infinity.

15. A proceas is reveraible ff it can be reversed such that both the system and the surroundings return to their original atates, with no other change anywhere elae in the universe.

Spontaneous processes of nature are irreversible. The idealised reveraible proceas is a quaai-static process with no diaeipative factora such as friction, viecoaity, etc.

14, Carnot engine is a reveraible engine operating between two temperatures T, (source) and T, (eink). The Carnot cycle consiste of two isothermal processes commected by two adiabatic processes. The efficiency of a Carnot engine is given by . 1 t a= “T (Carnot engined)

No engine operating between two temperatures can have efficiency greater than that of the Carnot engine.

16. If 9 > 0, heat ia added to the system If Q <0, heat is removed to the system If W > 0, Work is done by the system If W < 0, Work is done on the system

POINTS TO PONDER

1. Temperature of a body is related to its average internal energy, not to the kmetic energy of motion of its centre of mass. A bullet fired from a gun is not at a higher temperature because of its high speed.

2. Equilibrium in thermodynamics refers to the aituation when macroscopic variables describing the thermodynamic state of a system do not depend on time. Equilibrtum of @ system in mechanics means the uet external force and torque on the system are zero.

3. In a state of themmodynamic equilibrium, the microscopic constituents of a system are not in equilibrium (in the sense of mechanics).

4. Heat capacity, in general, depends on the process the system goes through when heat is supplied.

5. In isothermal quasi-static processes, heat is absorbed or gtven out by the system even though at every stage the gas has the same temperature as that of the surrounding reservoir. This is possible because of the tnfinttesimal difference in temperature between

the system and the reservotr.

EXERCISES

12.1 Ageyser heata water flowing at the rate of 3.0 litres per minute from 27 °C to 77 °C.If the geyser operates on a gas burner, what is the rate of consumption of the fuel if ita heat of combustion is 4.0 x 10° J/g ?

12.2 What amount of heat must be supplied to 2.0 x 107 kg of nitrogen (at room temperature) to raise its temperature by 45 °C at constant pressure ? (Molecular mass of N, = 28; R= 8.3 J mol" K".)

12.3 Explain why

(a) Two bodies at different temperatures T, and T, if brought in thermal contact do not necessarily settle to the mean temperature (T, + T,)/2.

(b) The coolant in a chemical or a nuclear plant @1.c., the liquid used to prevent the different parte of a plant from getting too hot) should have high specific heat.

(d) The climate of a harbour town is more temperate than that of a town in a desert at the same latitude.

12.4 Acylinder with a movable piston contains 3 moles of hydrogen at standard temperature and pressure, The walls of the cylinder are made of a heat insulator, and the piston ie insulated by having a pile of sand on it. By what factor does the pressure of the gas increase if the gas is compressed to half ite original volume 7?

12.5 In changing the state of a gas adiabatically from an equilibrium state A to another equilibrium state B, an amount of work equal to 22.3 J is done on the system. If the gas is taken from state A to B via a process in which the net heat absorbed by the syatem is 9.35 cal, how much ts the net work done by the system in the latter case 7

(Take 1 cal = 4.19 J)

12.8 Two cylinders A and B of equal capacity are connected to each other via a stopcock.Acontaine a gas at standard temperature and pressure. Bis completely evacuated.The entire system is thermally insulated. The stopcock is suddenly opened. Answer the following :

a) What is the final pressure of the gas in A and B?

(b) What is the change in internal energy of the gas ?

(d) Do the intermediate states of the system (before settling to the final equilibrium atate) He on ite P-V-T surface ?

12.7 Aeteam engine delivers 5.4x10°J of work per minute and services 3.6 x 10°J of heat per minute from its boiler. What is the efficiency of the engine? How much heat is wasted per minute?

12.8 An electric heater supplies heat to a system at a rate of 100W. If system performs work at a rate of 75 joules per second. At what rate ia the internal energy increasing?

12.8 Athermodynemic system is taken from an original state to an intermediate state by the linear process shown in Fig. (12.13)