5- STATES OF MATTER
STATES OF
MATTER
VERY SHORT QUESTIONS
ANSWER
Q.1.Name the three states of matter?
Ans. Solid, Liquid, Gas.
Q.2.Which state of matter is regarded
as condensed:gas or a solid?
Ans. Solid.
Q.3. Name the condensed states of
matter?
Ans. Solid and Liquid.
Q.4. Name four measurable properties of
gases?
Ans. Pressure, Volume, Temperature, and Moles (amount of
substance).
Q.5. Name the S.I. unit of pressure and
give its definition?
Ans. S.I. Unit of Pressure: Pascal (Pa)
Definition: 1 Pascal is equal to the pressure exerted by a force of 1
Newton per square meter.
Q.6. Why is air denser at lower lever
than at higher altitudes?
Ans. Gravity pulls air molecules towards the Earth's surface,
causing higher pressure and density at lower levels.
Q.7. Why is moist air lighter than dry
air?
Ans. Moist air is lighter than dry air because water vapor has
a lower molecular weight than the main components of dry air (nitrogen and
oxygen).
Q.8. State Boyle’s law of gases give
its mathematical expression?
Ans. Boyle's Law: The volume of a gas is inversely proportional to its
pressure, assuming the temperature remains constant.
Mathematical
Expression: PV = constant (where
P is pressure and V is volume)
Q.9. State Charles law?
Ans. Charles's Law: The volume of a gas is directly proportional to its
absolute temperature, assuming the pressure remains constant.
Q.10. Give mathematical expression for
Charles law?
Ans. V ∝ T (at constant pressure)
Q.11.Which is heavier: dry air or moist
air and why?
Ans. Moist air is heavier than dry air because water vapor
(which is present in moist air) has a higher molecular weight than the main
components of dry air (nitrogen and oxygen).
Q.12.Why is air dense at the sea level
Explain?
Ans. Air is dense at sea level due to the weight of the entire
atmosphere above pressing down on it.
Q.13. Carbon monoxide and nitrogen have
the same rates of diffusion why?
Ans. Carbon monoxide and nitrogen have the same rates of
diffusion because both gases have similar molecular masses and temperature.
Q.14.Molecular motion of a gas molecule
is termed as thermal motion comment?
Ans. molecular motion of a gas molecule is often referred to
as thermal motion because it is related to the kinetic energy associated with
temperature.
Q.15.What would have happened had the
molecular collisions between the gas molecules not been elastic?
Ans. If the molecular collisions between gas molecules were
not elastic, the gas would lose kinetic energy with each collision, resulting
in a loss of pressure and a decrease in temperature.
Q.16.Molecular motion of a gas molecule
is termed as thermal motion comment?
ANS. Yes, the molecular motion of a gas molecule is referred
to as thermal motion because it is driven by the kinetic energy associated with
temperature.
Q.17. Why jet aeroplanes flying at high
altitude need pressurization of cabins?
Ans. Jet airplanes flying at high altitudes need cabin
pressurization to maintain a breathable and comfortable environment for
passengers and crew.
Q.18.What are the S.I. units of surface tension?
Ans. Nm-1
Q.19.What is the difference between a
barometer and a manometer?
Ans. A barometer measures atmospheric pressure, while a
manometer measures the pressure of a confined gas or liquid.
Q.20.Can we make a liquid to boil at a
desired temperature?
Ans. Yes, we can make a liquid boil at a desired
temperature by adjusting the surrounding pressure.
Q.21.Which is Dalton‘s law of partial
pressure not applicable to a mixture of NH3 and HCI gases?
Ans. Dalton's law of partial pressure is not applicable to
a mixture of NH3 and HCl gases because they undergo a chemical reaction to form
ammonium chloride (NH4Cl) and no longer behave as separate gases.
Q.22.Which will have higher vapour
pressure—petrol or kerosene?
Ans. Petrol will have a higher vapor pressure than
kerosene.
Q.23.Why are aerated water bottles kept
under water during summer?
Ans. Aerated water bottles are kept under water during
summer to keep them cooler and prevent the carbon dioxide gas from escaping,
maintaining the carbonation.
Q.24. Why are aerated water bottles
kept under water during summer?
Ans. Aerated water bottles are kept under water during
summer to cool them quickly and reduce the risk of explosion due to excessive
pressure buildup from carbon dioxide gas.
Q.25.Liguid ammonia bottle is cooled
before opening the seal why?
Ans. Liquid ammonia bottle is cooled before opening the
seal to reduce the vapor pressure inside the bottle and prevent rapid gas
expansion, which could lead to a potential explosion.
Q.26.Sodium chloride pieces are harder
than sodium metal why?
Ans. Sodium chloride pieces are harder than sodium metal
due to their crystalline structure.
Q.27.Copper is more malleable and
ductile than brass why?
Ans. Copper is more malleable and ductile than brass due to
its simpler crystal structure and single metal composition.
Q.28.Define atmospheric pressure?
Ans. Atmospheric pressure is the force per unit area
exerted by the weight of the Earth's atmosphere on a surface.
Q.29.Given van der Waals ‘equation by
giving meaning of each term?
Ans. Atmospheric pressure is the force per unit area
exerted by the weight of the Earth's atmosphere on a surface.
Q.30.State Delton’s law of partial
pressure?
Ans. Dalton's law of partial pressure: Total pressure of a
gas mixture is the sum of the pressures of each individual gas in the mixture.
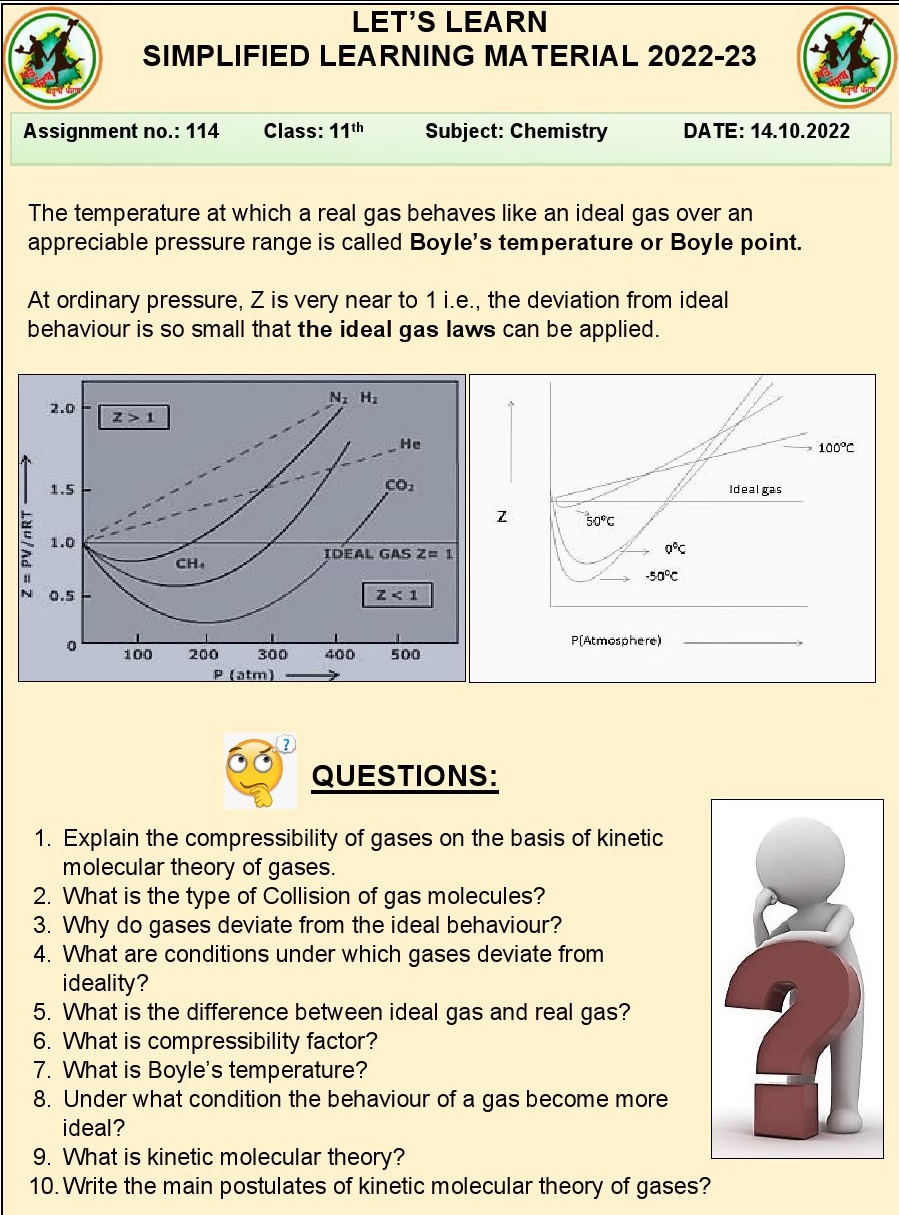
Q.31.What is meant by compressibility factor?
Ans. Compressibility factor: A dimensionless quantity
representing how much a real gas deviates from ideal gas behavior under
specific conditions.
Q.32.Define boiling point of a liquid?
Ans. Boiling
point: The temperature at which the vapor pressure of a liquid
becomes equal to the atmospheric pressure, causing the liquid to change into a
gas throughout the bulk of the liquid.
Q.33.What is the effect of pressure on viscosity
of a liquid Explain?
Ans. Increasing pressure generally decreases the viscosity
of a liquid due to the reduction of intermolecular spaces and enhanced
molecular motion.
Q.34.What is meant by elastic
collision?
Ans. Elastic
collision: A collision in which there is no net loss of kinetic
energy, and the total kinetic energy is conserved.
Q.35.Define aqueous tension?
Ans. Aqueous
tension: The partial pressure of water vapor in a gas mixture, usually
in the Earth's atmosphere.
Q.36.Waht are crystalline solids Give
examples?
Ans. Crystalline solids: Solids with a regular and
repeating arrangement of atoms, ions, or molecules in a well-defined
three-dimensional lattice.
Examples: Diamond,
Sodium chloride (table salt), Quartz.
Q.37.Why does solid NaCI not conduct
electricity?
Ans. Solid NaCl does not conduct electricity because its
ions are held in a fixed lattice structure and are not free to move, thus
preventing the flow of electric charge.
Q.38.Define critical temperature of gas
Give its expression?
Ans. Critical temperature of a gas: The temperature above
which the gas cannot be liquified, described by the Van der Waals equation as
Tc = (8a/27Rb).
Q.39.What is compressibility (Z) factor
for ideal gases?
Ans. Compressibility (Z) factor for ideal gases: Z = 1.
Q.40.Will the root mean square velocity
of N2 molecules change if it is mixed with argon at the same temperature?
Ans. No.
SHORT QUESTIONS ANSWER
Q.1.How will you explain nature of the
gas constant ‘R’?
Ans. The gas constant 'R' is a universal constant that
relates the properties of a gas to its behavior under different conditions,
such as pressure, volume, and temperature. It appears in various gas laws, like
the ideal gas law, and its value depends on the units used for pressure,
volume, and temperature. The value of 'R' remains constant for all gases and is
fundamental in connecting the macroscopic behavior of gases to their
microscopic properties at the molecular level.
Q.2.How will you calculate density of a
gas from ideal gas equation?
Ans. To calculate the density of a gas from the ideal gas
equation, you would need to rearrange the ideal gas equation and solve for
density (ρ).
The ideal gas equation is given as:
PV = nRT
Where:
P = Pressure of the gas
V = Volume of the gas
n = Number of moles of the gas
R = Gas constant
T = Temperature of the gas
To calculate density (ρ) from this equation, we need
to express density as mass per unit volume:
ρ = m/V
Where:
ρ = Density of the gas
m = Mass of the gas (in grams, for example)
V = Volume of the gas (in liters, for example)
Now, we need to relate the number of moles (n) to mass (m)
using the molar mass (M) of the gas:
n = m/M
Substituting this into the ideal gas equation:
PV = (m/M)RT
Now, rearrange to solve for density (ρ):
ρ = (m/V) = (m/M)P/RT
So, the density of the gas can be calculated using the molar
mass (M), pressure (P), volume (V), and temperature (T) of the gas, along with
the ideal gas constant (R).
Q.3.Which gas is more dense at 1.0
atmosphere and 298 K?
Ans. At 1.0 atmosphere and 298 K, the gas that is more
dense will be the one with a higher molar mass, as per the ideal gas equation:
PV = nRT
Since the pressure (P), volume (V), and temperature (T) are
constant for both gases, the gas with the higher molar mass will have more
moles (n) and, therefore, higher density.
So, the gas with a higher molar mass will be more dense at
1.0 atmosphere and 298 K.
Q.4.State and explain Dalton‘s law of
partial pressure?
Ans. Dalton's law of partial pressure states that in a
mixture of non-reacting gases, the total pressure exerted by the mixture is
equal to the sum of the pressures that each gas would exert if it were present
alone and occupied the same volume.
Mathematically, Dalton's law can be expressed as:
P_total = P_1 + P_2 + P_3 + ... + P_n
Where:
P_total is the total pressure of the gas mixture,
P_1, P_2, P_3, ..., P_n are the partial pressures of individual
gases in the mixture.
The key idea behind Dalton's law is that each gas in the
mixture behaves independently and exerts its own pressure as if it were the
only gas present. The total pressure of the mixture is the sum of these
individual pressures.
Dalton's law is particularly useful when dealing with gas
mixtures, such as air, where different gases make up a specific fraction of the
total pressure. It allows us to understand and calculate the contributions of
each gas to the overall pressure in a mixture.
Q.5.State and explain graham’s Law of
diffusion?
Ans. Graham's law of diffusion states that the rate of
diffusion of a gas is inversely proportional to the square root of its molar
mass. In other words, lighter gases diffuse faster than heavier gases.
Mathematically, Graham's law can be expressed as:
Rate of diffusion ∝ 1/√M
Where:
Rate of diffusion is the speed at which a gas diffuses,
M is the molar mass of the gas.
The law can also be written as:
Rate of diffusion of Gas A / Rate of diffusion of Gas B =
√(Molar mass of Gas B / Molar mass of Gas A)
Explanation:
The key idea behind Graham's law is that at the same
temperature and pressure, gas particles with lower molar mass move at higher
speeds compared to gas particles with higher molar mass. The lighter gas
molecules have a higher average kinetic energy, allowing them to move faster
and diffuse more rapidly through a medium.
This law is essential in understanding the behavior of gases
and is often applied in various practical situations, such as in the diffusion
of gases through porous membranes or in determining the relative rates of
effusion of gases.
Q.6.Calculate the volume of oxygen that
will diffuse in the same time as 60 ml of SO2.
Ans. To calculate the volume of oxygen that will diffuse in
the same time as 60 ml of SO2, we can use Graham's law of diffusion, which
states that the rate of diffusion of a gas is inversely proportional to the
square root of its molar mass.
Let's assume the molar mass of oxygen (O2) is M1 and the
molar mass of sulfur dioxide (SO2) is M2.
Rate of diffusion of Oxygen (R1) / Rate of diffusion of
Sulfur dioxide (R2) = √(Molar mass of Sulfur dioxide / Molar mass of Oxygen)
R1 / R2 = √(M2 / M1)
Since the time is the same for both gases, we can
write:
Volume of Oxygen (V1) / Volume of Sulfur dioxide (V2) = R1 /
R2
Volume of Oxygen (V1) = (R1 / R2) * Volume of Sulfur dioxide
(V2)
Now, let's assume the rate of diffusion of sulfur dioxide
(R2) is 1 (arbitrary unit). We need to find the rate of diffusion of oxygen
(R1) relative to sulfur dioxide, which is √(M2 / M1).
Given that the molar masses are approximately:
Molar mass of Oxygen (O2) ≈ 32 g/mol
Molar mass of Sulfur dioxide (SO2) ≈ 64 g/mol
R1 / 1 = √(64 / 32) = √2
R1 ≈ 1.41 (approximately)
Now, we know that the volume of oxygen (V1) will be
approximately 1.41 times the volume of sulfur dioxide (V2):
Volume of Oxygen (V1) ≈ 1.41 * 60 ml ≈ 84.6 ml
So, the volume of oxygen that will diffuse in the same time
as 60 ml of SO2 is approximately 84.6 ml.
Q.7.An unknown gas diffuses four time
faster than oxygen calculate molecular mass of gas?
Ans. To calculate the molecular mass of the unknown gas, we
can use Graham's law of diffusion, which states that the rate of diffusion of a
gas is inversely proportional to the square root of its molar mass.
Let's assume the molar mass of the unknown gas is M.
Given that the unknown gas diffuses four times faster than
oxygen (O2), we can write the ratio of their rates of diffusion:
Rate of diffusion of unknown gas (R1) / Rate of diffusion of
oxygen (R2) = 4
According to Graham's law, this rate ratio is equal to
the square root of the molar mass ratio:
√(Molar mass of oxygen / M) = 4
Now, let's find the molar mass of oxygen (O2), which is
approximately 32 g/mol.
√(32 / M) = 4
Solving for M:
32 / M = 4^2
M = 32 / 16
M = 2 g/mol
So, the molecular mass of the unknown gas is approximately 2
g/mol.
Q.8.How is root mean square velocity
related to average velocity and most probable velocity?
Ans. Root mean square (RMS) velocity, average velocity, and
most probable velocity are all related to the motion of particles in a gas.
Root Mean Square (RMS) Velocity:
RMS velocity is a measure of the average velocity of
particles in a gas. It is the square root of the average of the squared
velocities of all the gas particles. Mathematically, for a gas with N
particles, the RMS velocity (v_rms) is calculated as follows:
v_rms = sqrt((v₁² + v₂² + ... + vN²) / N)
where v₁, v₂, ..., vN are the individual velocities of each
particle.
Average Velocity:
Average velocity is the arithmetic mean of the velocities of
all the gas particles. It is calculated by summing up all the velocities and
then dividing by the total number of particles. Mathematically, for the same
gas with N particles, the average velocity (v_avg) is calculated as follows:
v_avg = (v₁ + v₂ + ... + vN) / N
Most Probable Velocity:
Most probable velocity is the velocity at which the highest
number of particles in the gas are moving. It is the peak of the
Maxwell-Boltzmann distribution, which describes the distribution of velocities
of particles in a gas at a given temperature. The formula for the most probable
velocity (v_mp) is:
v_mp = √(2 * k * T / m)
where k is the Boltzmann constant, T is the temperature of
the gas in Kelvin, and m is the mass of a gas particle.
Relationships:
RMS Velocity and Average Velocity:
The RMS velocity and average velocity are related by a
constant factor. For an ideal gas, the RMS velocity is related to the average
velocity as follows:
v_rms = √(3/2) * v_avg
So, the RMS velocity is always higher than the average
velocity, and the ratio between them is √(3/2) or approximately 1.225.
RMS Velocity and Most Probable Velocity:
For an ideal gas, the RMS velocity is also related to the
most probable velocity by a constant factor. The ratio between the RMS velocity
and the most probable velocity (v_mp) is:
v_rms = √(3/2) * v_mp
This means that the RMS velocity is approximately 1.225 times
the value of the most probable velocity.
In summary, the root mean square velocity is related to the
average velocity and the most probable velocity by constant factors (√(3/2)).
These relationships are specific to ideal gases and depend on the assumption
that the gas particles follow the Maxwell-Boltzmann distribution, which holds
true for most gases at normal conditions.
Q.9.What is the effect of increase of
temperature on Maxwell distribution of velocities?
Ans. The Maxwell-Boltzmann distribution describes the
distribution of velocities of particles in an ideal gas at a given temperature.
It is a probability distribution that shows the relative number of particles
with different velocities in the gas. When the temperature of the gas
increases, it has a significant effect on the Maxwell distribution of
velocities, leading to the following changes:
Increased Average Velocity:
As the temperature increases, the average velocity of the gas
particles also increases. This is because temperature is directly proportional
to the average kinetic energy of the gas particles. The higher the temperature,
the greater the average kinetic energy, and thus the faster the particles move
on average. This is evident in the Maxwell distribution as the peak of the
curve shifts towards higher velocities.
Shift of the Distribution:
When the temperature increases, the entire Maxwell
distribution shifts to higher velocities. The distribution becomes broader and
more spread out. This means that a greater proportion of particles have higher
velocities compared to lower velocities. The shape of the curve remains the
same, but it is stretched out along the velocity axis.
Higher Proportion of High-Speed Particles:
With an increase in temperature, the number of gas particles
with higher velocities increases. This is because higher temperatures
correspond to a larger fraction of particles possessing higher kinetic
energies. Consequently, the tail of the Maxwell distribution, which represents
the high-speed particles, extends further to the right.
Decreased Most Probable Velocity:
The most probable velocity (v_mp) is the velocity at which
the highest number of particles in the gas are moving. As the temperature
increases, the most probable velocity decreases. However, it's important to
note that even though the most probable velocity decreases, the average
velocity and the root mean square (RMS) velocity both increase with
temperature.
In summary, an increase in temperature affects the Maxwell
distribution of velocities by shifting the distribution to higher velocities,
increasing the average velocity, and increasing the proportion of high-speed
particles. At the same time, the most probable velocity decreases. These
changes reflect the relationship between temperature, kinetic energy, and the
velocities of gas particles in accordance with the Maxwell-Boltzmann
distribution.
Q.10.Calculate the rate of molecular
velocities of the molecules of an ideal gas when the temperature of the gas id
doubled?
Ans. To calculate the rate of molecular velocities of the
molecules of an ideal gas when the temperature of the gas is doubled, we can
use the fact that the root mean square (RMS) velocity of gas molecules is
directly proportional to the square root of the temperature. Mathematically,
this relationship is expressed as:
v_rms ∝ √T
where v_rms is the RMS velocity of the gas molecules and T is
the temperature of the gas.
If we double the temperature (T → 2T), the RMS velocity
(v_rms) will increase accordingly. Specifically, it will become:
v_rms(new) = √(2T)
The ratio of the new RMS velocity (v_rms(new)) to the
original RMS velocity (v_rms) can be expressed as:
v_rms(new) / v_rms = √(2T) / √T
Now, we can simplify this ratio:
v_rms(new) / v_rms = √(2T) / √T = √2
So, when the temperature of the gas is doubled, the rate of
molecular velocities (RMS velocity) of the gas molecules will increase by a
factor of √2 or approximately 1.414 times.
Q.11.Write significance and units of
van der Waals’ constants?
Ans. Van der Waals' constants are two parameters, denoted
as "a" and "b," that are used in the van der Waals equation
of state. This equation is an improvement over the ideal gas law and accounts
for the finite size of gas molecules and the intermolecular forces between
them. The van der Waals equation is given as:
(P + a(n/V)^2) (V - nb) = nRT
where:
P = pressure of the gas
V = volume of the gas
n = number of moles of the gas
T = temperature of the gas
R = gas constant
Now, let's look at the significance and units of the van der
Waals' constants:
Van der Waals' constant "a":
Significance:
The constant "a" represents the attractive forces between gas
molecules. It corrects the pressure term in the ideal gas law by reducing the
pressure due to these attractive forces. The attractive forces cause the gas
molecules to come closer together, resulting in lower pressure than would be
predicted by the ideal gas law.
Units: The units
of "a" depend on the units used for pressure, volume, and the gas
constant in the van der Waals equation. The most common units for "a"
are (L^2·atm/mol^2) or (m^6·Pa/mol^2).
Van der Waals' constant "b":
Significance: The
constant "b" represents the volume occupied by one mole of gas
molecules. It corrects the volume term in the ideal gas law by accounting for
the finite size of the gas molecules. Since gas molecules have a finite volume,
they take up space, leading to a decrease in the effective volume available for
the gas to occupy.
Units: The units
of "b" also depend on the units used for volume and the number of
moles of gas in the van der Waals equation. The most common units for
"b" are (L/mol) or (m^3/mol).
In summary, van der Waals' constants "a" and
"b" are used to adjust the ideal gas law to account for the
attractive forces between gas molecules (a) and the finite volume occupied by
gas molecules (b). The units of "a" are (L^2·atm/mol^2) or
(m^6·Pa/mol^2), while the units of "b" are (L/mol) or (m^3/mol).
Q.12.Why are tyres of automobiles
inflated to lesser pressure in summer than in winter?
Ans. The inflation pressure of automobile tires is
generally adjusted based on the outside temperature, and it is common practice
to inflate tires to a slightly lower pressure in summer than in winter. There
are a couple of reasons for this:
Temperature Effects on Tire Pressure:
The pressure inside a tire is directly related to the
temperature of the air inside the tire. As the temperature changes, the
pressure inside the tire also changes. In warmer weather, the air inside the
tire expands due to the increased temperature, leading to higher tire pressure.
Conversely, in colder weather, the air inside the tire contracts due to the
decreased temperature, resulting in lower tire pressure.
To maintain the recommended tire pressure for safety and
optimal performance, it is essential to adjust the tire pressure based on the
temperature. Inflating the tires to a slightly lower pressure in summer
compensates for the increase in pressure caused by the higher temperatures.
Optimal Tire Performance:
Tire manufacturers provide recommended tire pressure values
that are usually determined based on average temperatures and driving
conditions. In winter, when temperatures are colder, tires may lose some
pressure, and maintaining the recommended pressure helps ensure proper
traction, handling, and overall performance on icy or wet roads.
On the other hand, in hot summer weather, over-inflated tires
can be more prone to blowouts, reduce traction, and cause uneven tire wear. By
slightly reducing the tire pressure in summer, the tire's contact area with the
road increases, enhancing grip and stability.
It's important to note that the pressure adjustment between
seasons is usually minimal, and drivers should always refer to the vehicle's
manual or the tire manufacturer's recommendations for the proper tire pressure.
Regularly checking and maintaining the correct tire pressure based on the
prevailing weather conditions and driving requirements is crucial for tire
longevity, fuel efficiency, and overall safety on the road.
Q13.Liquid ammonia bottle is cooled
before opening the seal Explain?
Ans. Cooling a liquid ammonia bottle before opening the
seal is done for safety reasons. Ammonia is a pungent, colorless gas with a
strong odor, and it is commonly used in various industrial applications,
refrigeration, and as a cleaning agent. However, ammonia gas is also toxic and
can be harmful to human health if inhaled in high concentrations. Cooling the
ammonia bottle helps to minimize the risk of gas release and potential exposure
to the gas. Here's why it is done:
Pressure
Reduction: Ammonia is typically stored in pressurized containers
as a liquid. Cooling the bottle reduces the internal pressure of the ammonia
gas. When the pressure is lowered, the risk of a sudden release of gas upon
opening the seal is minimized. If the bottle is at a higher temperature,
opening the seal may cause a rapid release of gas due to an increase in pressure,
which can be hazardous.
Vaporization
Control: Ammonia has a relatively low boiling point (-33.34°C
or -28.012°F at atmospheric pressure). Cooling the bottle helps keep the
ammonia in its liquid state, preventing or reducing the amount of vapor that
can be released when the seal is opened. Liquid ammonia is less volatile and
easier to handle than its gaseous form.
Odor
Control: As mentioned earlier, ammonia has a strong, pungent
odor that can be irritating and harmful when inhaled. Cooling the bottle can
help to minimize the escape of gas and, therefore, the odor.
Safety
Precaution: Cooling the bottle is a safety precaution that reduces
the risk of accidents or injuries when handling ammonia. Proper handling and
storage of ammonia are essential to prevent leaks, spills, or exposures.
It is crucial to follow safety guidelines and protocols when
working with ammonia or any other potentially hazardous substances. This
includes using appropriate personal protective equipment (PPE), working in
well-ventilated areas, and having proper training and knowledge of the specific
properties and hazards associated with the substance. If there is a need to
handle or work with ammonia, it should be done with care and in accordance with
safety regulations and guidelines.
Q.14.Derive the relation between average
kinetic energy of gas and its absolute temperature?
Ans. To derive the relation between the average kinetic
energy of a gas and its absolute temperature, we'll start with the kinetic
theory of gases. According to this theory, the kinetic energy of gas molecules
is directly related to their absolute temperature. The average kinetic energy
(KE) of gas molecules is given by the following equation:
KE_avg = (3/2) * k * T
where:
KE_avg is the average kinetic energy of the gas molecules,
k is the Boltzmann constant (k ≈ 1.380649 × 10^-23 J/K), and
T is the absolute temperature of the gas in Kelvin.
Let's go through the derivation step by step:
Kinetic Energy of a Single Gas Molecule:
The kinetic energy of a single gas molecule is given by the
classical formula:
KE = (1/2) * m * v^2
where:
m is the mass of a gas molecule, and
v is the velocity of the gas molecule.
Distribution of Gas Molecule Velocities:
In a gas, there is a distribution of molecular velocities.
The distribution of velocities of gas molecules follows the Maxwell-Boltzmann
distribution, which describes the probability of finding molecules with
different velocities at a given temperature.
Average Kinetic Energy:
The average kinetic energy (KE_avg) of gas molecules can be
found by taking the average of the kinetic energies of all gas molecules. We
integrate the kinetic energy over all possible velocities, weighted by the
probability distribution of velocities:
KE_avg = ∫ (1/2) * m * v^2 * f(v) dv
where f(v) is the probability distribution function of
velocities, which is given by the Maxwell-Boltzmann distribution:
f(v) = (4π * (m / (2πkT))^1.5) * v^2 * e^(-mv^2 / 2kT)
Integrating the Expression:
To find the average kinetic energy, we perform the
integration from 0 to infinity, taking into account the velocity probability
distribution:
KE_avg = ∫ (1/2) * m * v^2 * (4π * (m / (2πkT))^1.5) * v^2 *
e^(-mv^2 / 2kT) dv
This integral can be solved to obtain the result:
KE_avg = (3/2) * k * T
This final expression shows that the average kinetic energy
of gas molecules is directly proportional to the absolute temperature of the
gas. It confirms the relationship between temperature and kinetic energy, which
is a fundamental concept in the kinetic theory of gases.
Q.15.Define surface tension and surface
energy write units also?
Ans. Surface
Tension: Surface tension is a property of liquids that arises
due to the cohesive forces between the molecules on the surface of the liquid. It
is defined as the force acting parallel to the surface of the liquid and
perpendicular to any line drawn on the surface. In simpler terms, it is the
tendency of the surface of a liquid to minimize its area and form a shape with
the least surface area possible.
Surface tension is responsible for several phenomena, such as
the formation of droplets, capillary action, and the ability of certain insects
to walk on water. The molecules at the surface of the liquid experience an
inward force due to the unbalanced cohesive forces, causing the surface to
behave like a stretched elastic membrane.
Units
of Surface Tension: The SI unit of surface tension is
the newton per meter (N/m) or equivalently the joule per square meter (J/m^2).
Surface Energy:
Surface energy is the energy required to increase the surface
area of a liquid or solid. It is closely related to surface tension. The
concept of surface energy can be applied to both liquids and solids, and it
quantifies the energetic cost of creating new surfaces.
For liquids, surface energy is synonymous with surface
tension, as it represents the energy required to create a new unit area of the
liquid surface. For solids, surface energy refers to the energy required to
increase the surface area of the solid material.
Units
of Surface Energy: The units of surface energy are
also joules per square meter (J/m^2) or equivalently newton per meter (N/m).
In summary, surface tension is the force acting on the
surface of a liquid due to the cohesive forces between its molecules, and it is
measured in newton per meter (N/m) or joules per square meter (J/m^2). Surface
energy, on the other hand, is the energy required to increase the surface area
of a liquid or solid and is also measured in newton per meter (N/m) or joules
per square meter (J/m^2). Both surface tension and surface energy play
essential roles in various natural phenomena and engineering applications.
Q.16. How will you measure the surface
tension of a liquid?
Ans. Measuring the surface tension of a liquid typically involves
conducting an experiment using specialized instruments. There are various
methods to measure surface tension, but one common approach is the
"capillary rise method." Here's a step-by-step guide on how to
measure the surface tension of a liquid using this method:
Materials Needed:
A clean and dry capillary tube (narrow glass tube)
A container to hold the liquid
A ruler or measuring tape
A stopwatch or timer
A balance (to measure the mass of the liquid)
Procedure:
Clean the Capillary Tube:
Ensure that the capillary tube is clean and free from any
contaminants or residues. Use a suitable cleaning method, such as rinsing it
with a cleaning agent and distilled water, then allow it to dry completely.
Measure the Inner Diameter of the Capillary Tube:
Using a ruler or a micrometer, measure the inner diameter (d)
of the capillary tube. Make sure to record this value, as it is crucial for
calculating the surface tension later.
Determine the Density of the Liquid:
Measure the mass (m) of an empty, dry container. Then, add a
known volume of the liquid to the container and measure the combined mass (m +
Δm). Calculate the mass of the liquid (Δm) by subtracting the mass of the empty
container from the combined mass. Divide this mass by the volume of the liquid
(V) to find the density (ρ) of the liquid:
ρ = Δm / V
Prepare the Liquid Sample:
Fill the container with the liquid, making sure it is free
from bubbles or impurities.
Perform the Capillary Rise Experiment:
Hold the capillary tube vertically and immerse one end of it
into the liquid. The liquid will rise in the capillary tube due to capillary
action. Allow the liquid to stabilize and rise to a certain height (h) in the
capillary tube.
Measure the Capillary Rise:
Using the ruler or measuring tape, measure the height (h) to
which the liquid rises in the capillary tube.
Calculate the Surface Tension:
Finally, use the following formula to calculate the surface
tension (γ) of the liquid:
γ = (2 * ρ * g * h) / d
where:
γ = Surface tension of the liquid
ρ = Density of the liquid
g = Acceleration due to gravity (approximately 9.81 m/s²)
h = Capillary rise height
d = Inner diameter of the capillary tube
It's important to note that the capillary rise method
provides an indirect measurement of surface tension and assumes that the liquid
behaves like an ideal liquid in a capillary tube. Additionally, to obtain
accurate results, it's essential to repeat the experiment multiple times and
take the average of the measurements.
Q.17.Distinguish between ldeal gas and
real gas?
Ans. Ideal Gas:
Definition: An ideal
gas is a theoretical concept that follows the ideal gas law at all conditions
of pressure and temperature. It is an imaginary gas that exhibits certain
idealized behaviors, making its behavior simpler and easier to analyze in
theoretical calculations.
Assumptions:
a. The gas molecules have negligible volume compared to the
volume of the container they occupy.
b. There are no intermolecular forces or attractions between
gas molecules.
c. Gas molecules undergo completely elastic collisions with
each other and the container walls.
d. The average kinetic energy of gas molecules is directly
proportional to the absolute temperature.
Behavior:
a. An ideal gas obeys the ideal gas law: PV = nRT, where P is
the pressure, V is the volume, n is the number of moles of the gas, R is the
ideal gas constant, and T is the absolute temperature in Kelvin.
b. At low pressures and high temperatures, real gases tend to
behave more like ideal gases.
Real Gas:
Definition: Real gases
are actual gases that do not perfectly follow the assumptions of the ideal gas
law. They deviate from ideal behavior under certain conditions, especially at
high pressures and low temperatures.
Assumptions:
a. Real gases have non-negligible volume, and the volume of
the gas molecules is significant compared to the volume of the container.
b. There are intermolecular forces or attractions between gas
molecules.
c. Gas molecules may experience non-elastic collisions and
interactions with each other and the container walls.
d. The behavior of real gases is more accurately described by
the van der Waals equation or other more complex equations of state.
Behavior:
a. Real gases do not strictly follow the ideal gas law at all
conditions. Deviations occur at high pressures, where the volume of the gas
molecules becomes significant, and at low temperatures, where intermolecular
forces become more significant.
b. The van der Waals equation of state accounts for the
non-ideal behavior of real gases and includes correction terms for the volume
of the gas molecules and the intermolecular forces.
In summary, the main difference between an ideal gas and a
real gas lies in their behavior with respect to the ideal gas law and the
assumptions made about their molecular properties. Ideal gases are theoretical
and obey the ideal gas law perfectly, while real gases are actual gases that
deviate from ideal behavior due to non-negligible molecular volume and
intermolecular forces. To describe the behavior of real gases, more complex
equations, such as the van der Waals equation, are used.
Q.18.Write some important postulates of
kinetic molecular theory of gas?
Ans. The kinetic molecular theory of gases is a fundamental
concept in understanding the behavior of gases. It is based on several
postulates that describe the properties and behavior of gas molecules. Here are
some important postulates of the kinetic molecular theory of gases:
Gas
consists of particles: The theory assumes that gases are
composed of a large number of small particles, often referred to as gas
molecules or atoms. These particles are in constant, random motion and are
widely spaced apart relative to their size.
Particles
have negligible volume: The volume occupied by the gas
particles themselves is assumed to be negligible compared to the volume of the
entire gas sample. This means that gas molecules are treated as point masses
with no significant volume.
Particles
are in constant motion: Gas molecules are in continuous,
rapid, and random motion. They move in straight lines until they collide with
other molecules or the walls of the container.
Elastic
collisions: Gas molecules undergo perfectly elastic collisions with each
other and the walls of the container. In an elastic collision, there is no net
loss of kinetic energy, and the total kinetic energy of the gas remains
constant.
No
intermolecular forces: The kinetic molecular theory
assumes that there are no intermolecular forces or attractions between gas
molecules. This is why gases tend to spread out and fill the entire volume of
the container they occupy.
Kinetic energy is directly proportional to temperature: The
average kinetic energy of gas molecules is directly proportional to the
absolute temperature of the gas. As the temperature increases, the molecules
gain kinetic energy and move faster.
Average kinetic energy is the same for all gases at the same
temperature: At the same temperature, all gas molecules, regardless of their
masses, have the same average kinetic energy per molecule.
Pressure
is the result of molecular collisions: The
pressure exerted by a gas is the result of the constant collisions of gas
molecules with each other and the walls of the container. The force of these
collisions gives rise to pressure.
Gas behavior is ideal at low pressure and high temperature:
Under conditions of low pressure and high temperature, gas molecules behave
most closely to the predictions of the ideal gas law, which is derived from the
kinetic molecular theory.
These postulates form the foundation of the kinetic molecular
theory of gases and provide a simple yet powerful model for understanding the
macroscopic behavior of gases based on the behavior of individual gas molecules.
Q.19.How do amorphous solids differ
from crystalline solids?
Ans. Amorphous solids and crystalline solids are two distinct
types of solids that differ in their atomic or molecular arrangement and their
overall properties. Here are the key differences between amorphous solids and
crystalline solids:
Atomic/Molecular Arrangement:
Amorphous
Solids: In amorphous solids, the atoms, ions, or molecules are
arranged in a random and disordered fashion. There is no long-range order in
the arrangement, and the structure lacks a repeating pattern. As a result, the
atomic arrangement in amorphous solids is similar to that of liquids, but they
have a fixed shape and do not flow like liquids.
Crystalline
Solids: In crystalline solids, the atoms, ions, or molecules
are arranged in a highly ordered and repetitive three-dimensional pattern. This
repeating pattern extends throughout the entire solid, forming a crystal
lattice. The presence of long-range order gives crystalline solids distinct
faces and sharp edges, and they exhibit well-defined geometric shapes.
Melting Behavior:
Amorphous
Solids: Amorphous solids do not have a sharp melting point.
Instead, they soften gradually over a range of temperatures, typically called
the glass transition temperature. When heated, amorphous solids transform into
a supercooled liquid and then slowly become more fluid-like as the temperature
continues to rise.
Crystalline
Solids: Crystalline solids have a well-defined melting point.
At this specific temperature, the crystal lattice breaks down, and the solid
undergoes a phase change to become a liquid.
Transparency and Opacity:
Amorphous
Solids: Amorphous solids are often transparent or translucent,
allowing light to pass through, but they can also be opaque depending on their
composition.
Crystalline
Solids: Crystalline solids can be transparent, translucent, or
opaque, depending on the arrangement of their crystal lattice and the nature of
the atomic/molecular interactions.
Mechanical Properties:
Amorphous Solids: Amorphous solids typically have a lower
hardness and are less rigid than crystalline solids. They are often less
brittle and more prone to undergo plastic deformation.
Crystalline
Solids: Crystalline solids tend to have a higher hardness and
are more rigid and brittle due to the regular arrangement of their atoms or
molecules.
Examples:
Amorphous
Solids: Examples of amorphous solids include glass, rubber,
plastics, and some types of gels.
Crystalline
Solids: Examples of crystalline solids include diamond,
quartz, table salt (sodium chloride), and metals like iron and copper.
In summary, amorphous solids have a disordered atomic
arrangement, lack a specific melting point, and often have lower hardness and
rigidity compared to crystalline solids, which have a highly ordered structure,
a well-defined melting point, and greater hardness and rigidity.
Q.20.Write the units of gas constant R
in different scales of measurement?
Ans. The gas constant (R) is a fundamental constant in the
ideal gas law and is used to relate the properties of gases, such as pressure,
volume, temperature, and the number of moles. The units of the gas constant
depend on the scale of measurement used for pressure, volume, and temperature.
Here are the units of the gas constant R in different scales of measurement:
Ideal Gas Law in SI Units:
In the International System of Units (SI), the units
of the gas constant R are as follows:
R = 8.314 J/(mol·K)
Where:
J = joule (the SI unit of energy)
Mol = mole (the SI unit of the amount of substance)
K = Kelvin (the SI unit of temperature)
Ideal Gas Law in CGS Units:
In the centimeter-gram-second (CGS) system, the units of the
gas constant R are given as:
R = 8.314 × 10^7 erg/(mol·K)
Where:
Erg = erg (the CGS unit of energy)
Ideal Gas Law in Imperial Units:
In the Imperial system (commonly used in the United States),
the units of the gas constant R are as follows:
R = 1.987 cal/(mol·K)
Where:
Cal = calorie (the unit of energy commonly used in chemistry)
It's important to note that the gas constant R is a universal
constant, and its numerical value remains the same regardless of the units used
for pressure, volume, and temperature, as long as these units are consistent
with each other. However, it's essential to use the appropriate units for all
variables when applying the gas constant in specific calculations to ensure accurate
and consistent results.
Q.21.Describe the four types of
crystalline solids?
Ans. Crystalline solids can be classified into four main
types based on their different structural arrangements of atoms, ions, or
molecules in their crystal lattice. The four types of crystalline solids are:
Ionic Crystals:
Ionic crystals are composed of positively charged ions
(cations) and negatively charged ions (anions) held together by strong
electrostatic forces. These forces result from the attraction between opposite
charges. Ionic crystals have a three-dimensional lattice structure, with each
ion surrounded by ions of the opposite charge. The arrangement of ions forms
repeating patterns, and the crystal lattice is very stable. Examples of ionic
crystals include sodium chloride (table salt) and potassium nitrate
(saltpeter).
Covalent Network Crystals:
Covalent network crystals are composed of atoms that are
covalently bonded to each other in a three-dimensional network. Each atom forms
strong covalent bonds with neighboring atoms, creating a continuous and
interconnected network throughout the crystal. These covalent bonds are very
strong, making covalent network crystals hard and with high melting points.
Examples of covalent network crystals include diamond, graphite, and silicon
dioxide (quartz).
Metallic Crystals:
Metallic crystals consist of a regular arrangement of metal
atoms in a crystal lattice. In metallic bonding, the valence electrons of metal
atoms are delocalized, forming an electron sea that allows the atoms to share
electrons freely. This delocalization of electrons gives metals their
characteristic properties, such as electrical and thermal conductivity and
malleability. Examples of metallic crystals include copper, iron, and aluminum.
Molecular Crystals:
Molecular crystals are composed of discrete molecules held
together by weak van der Waals forces or hydrogen bonds. These forces are much
weaker than ionic or covalent bonds, leading to lower melting points and softer
structures. The molecules in molecular crystals are often polar or have
dipoles, which can give rise to unique properties like piezoelectricity and
ferroelectricity. Examples of molecular crystals include solid water (ice),
sulfur, and organic compounds like naphthalene and sucrose (sugar).
Each type of crystalline solid exhibits distinct properties
and behavior based on the nature of the bonding and the arrangement of atoms,
ions, or molecules in their crystal lattice. Understanding the different types
of crystalline solids is essential in materials science, chemistry, and
physics, as it helps to explain a wide range of properties and applications of
various materials.
Q.22.Describe different types of
molecular how are these related to the temperature?
Ans. Molecular interactions play a crucial role in
determining the properties and behavior of substances. Depending on the type of
molecular interactions, substances can be classified into different states of
matter: solids, liquids, and gases. The state of matter is closely related to
the temperature of the substance. Let's describe the different types of
molecular interactions and their relationship with temperature:
Solid State:
In a solid, molecules are held together by strong
intermolecular forces, such as covalent bonds, ionic bonds, or metallic bonds.
The molecules in a solid are tightly packed and have fixed positions, forming a
rigid and ordered three-dimensional lattice. Due to the strong forces holding
the molecules together, solids have a definite shape and volume. As the
temperature increases, the kinetic energy of the molecules also increases,
causing them to vibrate more vigorously around their fixed positions. However,
the intermolecular forces are still strong enough to keep the molecules in
their lattice positions, and the solid retains its shape and structure.
Liquid State:
In a liquid, molecules are held together by weaker
intermolecular forces compared to a solid. The molecules have more freedom of
movement, allowing them to flow past one another. As the temperature increases,
the kinetic energy of the molecules increases, leading to more rapid and random
movement. At higher temperatures, the intermolecular forces become weaker, and
the liquid can transition into a gas state through vaporization. The transition
from a liquid to a gas is known as boiling or evaporation, depending on the
temperature and pressure.
Gaseous State:
In a gas, molecules have very weak intermolecular forces and
move freely and independently of one another. The kinetic energy of the
molecules in a gas is high, causing them to move rapidly and randomly in all
directions. As the temperature increases, the kinetic energy of the gas
molecules increases further, leading to an increase in their average speed and
the overall pressure of the gas. At extremely high temperatures, a gas may
undergo ionization and become a plasma, where the atoms or molecules dissociate
into charged particles.
In summary, the type of molecular interactions and the state
of matter of a substance depend on the strength of the intermolecular forces.
As the temperature increases, the kinetic energy of the molecules increases,
affecting the strength of these forces. At low temperatures, molecules may be
held together more tightly in a solid or liquid state. As the temperature
rises, the intermolecular forces weaken, leading to a transition from a solid
to a liquid or from a liquid to a gas. Ultimately, at high temperatures, the
molecules have enough kinetic energy to overcome the intermolecular forces entirely,
resulting in a gas or even a plasma state.
Q.23. How will you modify graham‘s law
of diffusion in terms of molecular
masses, rate and yolume?
Ans. Graham's law of diffusion describes the relationship
between the rates of diffusion of two gases. It states that the rate of
diffusion of a gas is inversely proportional to the square root of its molar
mass. Mathematically, Graham's law can be expressed as:
Rate1 / Rate2 = √(Molar Mass2 / Molar Mass1)
Where:
Rate1 and Rate2 are the rates of diffusion of gases 1 and 2,
respectively.
Molar Mass1 and Molar Mass2 are the molar masses of gases 1
and 2, respectively.
To modify Graham's law in terms of molecular masses, rate,
and volume, we need to consider the relationship between molar mass, molecular
mass, and volume of gases. The molar mass of a gas is the mass of one mole of
gas molecules, while the molecular mass refers to the mass of one molecule of
the gas.
Let's assume we have two gases with molar masses M1 and M2,
molecular masses m1 and m2, rates of diffusion D1 and D2, and volumes V1 and
V2.
The relationship between molar mass (M) and molecular mass
(m) can be expressed as:
M = m * NA
Where:
NA is Avogadro's number (6.022 x 10^23 mol^-1).
Now, let's modify Graham's law in terms of molecular masses, rate,
and volume:
(D1 / D2) = √[(M2 / V2) / (M1 / V1)] * √(m1 / m2)
Explanation:
We know from Graham's law that (Rate1 / Rate2) = √(Molar
Mass2 / Molar Mass1). To modify the equation, we replace the molar masses with
(M1 / V1) and (M2 / V2), as the molar mass is related to molecular mass and
volume.
We also know that M = m * NA. So, (M2 / M1) = (m2 * NA) / (m1
* NA), which simplifies to √(m2 / m1).
Combining the two modifications, we get:
(D1 / D2) = √[(M2 / V2) / (M1 / V1)] * √(m1 / m2)
This modified version of Graham's law takes into account the
relationship between molecular masses, rate, and volume of gases and provides a
more comprehensive expression for the diffusion rates of gases based on their
properties.
Q.23.Lassaigne’s extract is prepared in
distilled water and not in tap water Explain?
Ans. Lassaigne's extract is a solution used in analytical
chemistry to test for the presence of certain elements, particularly nitrogen,
sulfur, and halogens (chlorine, bromine, and iodine), in organic compounds. It
is prepared by fusing the organic compound with a small amount of sodium metal
and then extracting the resulting mixture with water.
The reason why Lassaigne's
extract is prepared in distilled water and not in tap water is to avoid any
potential interference or contamination from impurities present in tap water.
Distilled water is purified through the process of distillation, where water is
heated to vaporize and then condensed back into liquid form, leaving behind
most impurities and contaminants. As a result, distilled water is relatively
free from dissolved minerals, ions, and other impurities that could react with
the organic compound or interfere with the tests being conducted.
On the other hand, tap water
may contain various dissolved minerals, chlorine, fluoride, and other
substances that could potentially react with the organic compound or the sodium
metal during the fusion process. These impurities could lead to false-positive
or false-negative results in the tests for nitrogen, sulfur, and halogens.
Using distilled water
ensures that the water used in the preparation of Lassaigne's extract is of
high purity and will not introduce any unwanted substances that could affect
the accuracy and reliability of the analytical tests. It is a standard practice
in analytical chemistry to use reagents and solvents of high purity to minimize
potential sources of errors and ensure the validity of the experimental
results.
Q.24. Lassaigne’s test is not very
useful in case of diazonium salts explain?
Ans. Lassaigne's test is a chemical test used to detect the
presence of nitrogen, sulfur, and halogens in organic compounds. It involves
fusing the organic compound with sodium metal to convert these elements into
water-soluble sodium compounds. The resulting mixture is then extracted with
water, and specific reagents are added to test for the presence of these
elements.
However, Lassaigne's test is
not very useful in the case of diazonium salts. Diazonium salts are a class of
organic compounds that contain a positively charged nitrogen atom (diazo group,
-N2+) directly attached to an aromatic ring. The general structure of a
diazonium salt is R-N2+ X-, where R is an aromatic group and X is an anion,
such as chloride (Cl-), bromide (Br-), or tetrafluoroborate (BF4-).
The reason Lassaigne's test
is not useful for diazonium salts is because the nitrogen in diazonium salts is
already in the form of a positively charged cation (-N2+). During the fusion
step of Lassaigne's test, the diazonium cation is highly unstable and tends to
decompose explosively into nitrogen gas (N2) and a highly reactive carbocation.
This explosive decomposition
of diazonium salts during the fusion process makes it difficult to extract and
isolate the nitrogen-containing species for further testing. Additionally, the
nitrogen atom in diazonium salts is not converted into a water-soluble compound
during the fusion with sodium metal, further complicating the detection
process.
As a result of these
challenges, Lassaigne's test is not suitable for detecting nitrogen in the form
of diazonium salts. Instead, specific tests and techniques, such as the
Sandmeyer reaction or the coupling reaction with an aromatic compound, are used
to identify and characterize diazonium salts in organic chemistry. These
methods are more suitable for working with these highly reactive and unstable
species and provide more reliable results in detecting the presence of
diazonium salts.