CHAPTER 2 STRUCTURE OF ATOM

VERY SHORT QUESTIONS ANSWER

Q.1.What happens when a high voltage is passed through air in discharge tube at low pressure?

Ans. Plasma.

Q.2.How can you say cathode rays consist of negatively charge particles?

Ans. Deflection.

Q.3.What happens when an electric discharge is passed through a gas in discharge tube fitted with a perforated cathode?

Ans. Glow.

Q.4.What is an electron and who discovered it?

Ans. Subatomic. J.J. Thomson.

Q.5.What are protons and who discovered protons?

Ans. Positive. Ernest Rutherford.

Q.6.What is neutron and who discovered it?

Ans. Neutral. James Chadwick.

Q.7. Define atomic number?

Ans. Number of protons.

Q.8. Define mass number?

Ans. Total protons and neutrons.

Q.9.What do you understand by dual nature of radiations?

Ans. Wave-particle duality of radiations means that electromagnetic radiation, such as light, exhibits both wave-like and particle-like properties simultaneously.

Q.10.What is dual nature of Electrons?

Ans. Wave-particle duality of electrons means that electrons, like other subatomic particles, exhibit both wave-like and particle-like properties simultaneously.

Q.11.What is photoelectric effect?

Ans. Emission.

Q.12.What are electromagnetic radiations? Give two examples?

Ans. Light waves. Examples: Visible light and radio waves.

Q.13. Define (A) frequency (B) wavelength?

Ans. (A) Frequency: Number of cycles per unit time, usually measured in Hertz (Hz).

(B) Wavelength: Distance between two consecutive points in a wave that are in phase, typically measured in meters (m).

Q.14. How is photon different from proton?

Ans. Photon: Particle of electromagnetic radiation with no mass and no electric charge.

Proton: Subatomic particle with positive charge found in the nucleus of an atom and has mass.

Q.15.Name the element whose isotope has mass number 14 and 8 neutrons?

Ans. Oxygen.

Q.16.State Heisenberg‘s uncertainty principle?

Ans. Uncertainty principle: Simultaneous measurement.

Q.17. Define pauli Exclusion principle?

Ans. Exclusion: Two identical fermions.

Q.18. Define Hund‘s rule of maximum multiplicity?

Ans. Maximum: Electrons occupy.

Q.19. Define Aufbau principle?

Ans. Aufbau: Electrons fill.

Q.20.What is the relationship between wavelength and momentum of a particle?

Ans. Inverse.

Q.21.Which quantum number specifies the shape of an orbital?

Ans. The quantum number that specifies the shape of an orbital is the azimuthal quantum number, also known as the angular momentum quantum number (l).

Q.22. By what name is the following principle known Electrons with the same spin quantum number cannot be present in the same atomie orbital?

Ans. Pauli Exclusion Principle.

Q.23.Which quantum number will express the difference in two electrons in k-shell?

Ans. The magnetic quantum number (m) expresses the difference in two electrons in the K-shell.

Q.24.Name the phenomena that indicate the dual nature of electrons?

Ans. The phenomenon that indicates the dual nature of electrons is the electron diffraction.

Q.25.Why can we not assign a definite line path to a moving electron?

Ans. Wave-particle duality.

Q.26.How does change in velocity of a moving particle alter the wavelength related to the particle?

Ans. As the velocity of a moving particle increases, its wavelength decreases (and vice versa) according to the de Broglie wavelength equation.

Q.27.What is the significance of angular quantum number?

Ans. Shape of orbitals.

Q.28.Which quantum number determines the orientation of an atomic orbital?

Ans. The magnetic quantum number determines the orientation of an atomic orbital.

Q.29.Which quantum number is linked to the shape of an orbital in an atom?

Ans. The azimuthal quantum number is linked to the shape of an orbital in an atom.

Q.30.Which quantum number determines the energy associated with an orbital in an atom?

Ans. The principal quantum number determines the energy associated with an orbital in an atom.

Q.31.Why can the motion of an electron around the nucleus not be determined accurately?

Ans. Due to the inherent wave-like nature of electrons in quantum mechanics, their exact position and velocity cannot be simultaneously determined accurately. This limitation is described by Heisenberg's Uncertainty Principle.

Q.32. Define an atomic orbital what does angular momentum quantum number tall about an orbital?

Ans. Atomic orbital: Region around the nucleus where electrons are likely to be found.

 

Angular momentum quantum number: Describes the shape and type of orbital (s, p, d, f) in an atom.

 

Q.34.Give the maximum number of electrons which can be accommodated in a set of (A) P- orbitals and (B) d-orbitals.

Ans. (A) P-orbitals: The maximum number of electrons that can be accommodated in a set of P-orbitals is 6 (2 electrons in each of the three P orbitals).

(B) D-orbitals: The maximum number of electrons that can be accommodated in a set of D-orbitals is 10 (2 electrons in each of the five D orbitals).

Q.35.What is the nature of VIBGYOR?

Ans. VIBGYOR refers to the colors of the visible light spectrum. It stands for Violet, Indigo, Blue, Green, Yellow, Orange, and Red. These are the colors that can be seen by the human eye when white light is dispersed or refracted, such as through a prism.

Q.36. What values are permitted for the angular momentum quantum number I for an electron with principal quantum number , n =4?

Ans. For an electron with principal quantum number (n) = 4, the permitted values for the angular momentum quantum number (l) can be 0, 1, 2, or 3. These correspond to the different subshells with shapes s, p, d, and f, respectively.

Q.37.Which quantum number specifies the energy if an electron in an atom?

Ans. The principal quantum number (n) specifies the energy of an electron in an atom.

Q.38. Why do may elements have fractional atomic masses?

Ans. Many elements have fractional atomic masses due to the presence of isotopes, which have different masses and abundances, contributing to the weighted average.

Q.39.When do electrons from various energy levels fall to first energy level in hydrogen Name the series of spectral lines?

Ans. Electrons from various energy levels fall to the first energy level in hydrogen during electronic transitions, producing the Lyman series of spectral lines.

Q.40.What is meant by quantisation of energy?

Ans. Quantization of energy refers to the concept that energy levels in certain physical systems are discrete and can only take specific, quantized values, rather than having continuous values.

SHORT QUESTIONS ANSWER

Q.1.What was Thomson, s plum pudding model of an atom?

Ans. Thomson's plum pudding model of an atom, proposed in the early 20th century, suggested that the atom is a uniform, positively charged sphere with negatively charged electrons embedded within it like plums in a pudding. It implied that the negative and positive charges were evenly distributed throughout the atom. However, this model was later replaced by the more accurate Rutherford model.

Q.2.What do you mean by jnterference and diffraction?

Ans. Interference and diffraction are both phenomena that occur when waves interact with each other or with obstacles.

Interference: Interference is the phenomenon that takes place when two or more waves combine and their amplitudes either reinforce (constructive interference) or cancel out (destructive interference) at specific points in space. It occurs when waves overlap, leading to a new wave pattern.

 

Diffraction: Diffraction is the bending or spreading of waves as they encounter obstacles or pass through narrow openings. It occurs when waves encounter an obstacle that is comparable in size to their wavelength, causing the waves to change direction and spread out beyond the obstacle's edges. Diffraction is more prominent with waves of longer wavelengths, such as sound waves or water waves.

Q.3.Calculat the number of electrons which will together weigh one gram?

Ans. To calculate the number of electrons that together weigh one gram, we need to use the mass of a single electron and Avogadro's constant.

Mass of a single electron (m_e) ≈ 9.109 x 10^-31 kg

Avogadro's constant (N_A) ≈ 6.022 x 10^23 mol^-1

We know that 1 gram is equal to 0.001 kg.

Now, let's find the number of electrons:

Number of electrons = (1 gram) / (mass of a single electron)

Number of electrons = (0.001 kg) / (9.109 x 10^-31 kg)

Number of electrons ≈ 1.099 x 10^26 electrons

So, approximately 1.099 x 10^26 electrons will together weigh one gram.

Q.4.What do you mean by electromagnetic spectrum?

Ans. The electromagnetic spectrum refers to the entire range of electromagnetic waves, which are a form of energy that travels in the form of waves at the speed of light. It encompasses a broad range of frequencies and wavelengths, from the longest radio waves to the shortest gamma rays.

The electromagnetic spectrum includes various types of waves, such as:

Radio waves

Microwaves

Infrared radiation

Visible light

Ultraviolet radiation

X-rays

Gamma rays

Each of these waves has different properties and applications. Visible light is the portion of the electromagnetic spectrum that can be seen by the human eye, while other types of waves have applications in communications, imaging, heating, medical treatments, and scientific research.

Q.5.What do you mean by Heisenberg ’s uncertainty principle?

Ans. Heisenberg's uncertainty principle is a fundamental concept in quantum mechanics, formulated by the German physicist Werner Heisenberg in 1927. It states that it is impossible to simultaneously know both the exact position (location) and the exact momentum (velocity) of a subatomic particle, such as an electron.

In other words, the more precisely we try to measure the position of a particle, the less precisely we can determine its momentum, and vice versa. This principle arises from the wave-like nature of particles at the quantum level, where their properties are described by probability distributions rather than definite values.

Heisenberg's uncertainty principle has profound implications for our understanding of the behavior of subatomic particles and places limitations on the accuracy of measurements in the microscopic world. It represents a fundamental uncertainty in our knowledge of quantum systems and is a cornerstone of quantum mechanics.

Q.6. Why is Heisenberg’s uncertainty principle not useful in daily life?

Ans. Heisenberg's uncertainty principle is not useful in daily life for several reasons:

 

It is applicable at the quantum level: Heisenberg's uncertainty principle applies to particles at the atomic and subatomic scale. In our daily lives, we deal with macroscopic objects where quantum effects are negligible.

Macroscopic objects have well-defined properties: In everyday situations, the objects we interact with have well-defined positions and momenta in classical physics. The uncertainty principle becomes significant only when dealing with extremely small particles, such as electrons and photons.

Quantum effects are typically not observable: Quantum effects become prominent when dealing with particles with very short wavelengths, which are far beyond our ability to observe or manipulate in daily life.

Technological limitations: Measuring devices and methods in our daily lives are not sensitive enough to detect the minute uncertainties predicted by the uncertainty principle at the quantum level.

Overall, the uncertainty principle's effects are confined to the realm of the very small and do not have practical implications in our daily experiences with the macroscopic world. It remains a crucial concept for understanding quantum mechanics and the behavior of subatomic particles in the realm of modern physics and technology.

Q.7. Give important postulates of Planck‘s quantum theory of radiation?

Ans. Planck's quantum theory of radiation, proposed by Max Planck in 1900, laid the foundation for quantum mechanics and explained the behavior of blackbody radiation. The important postulates of Planck's quantum theory are:

Energy Quantization: Planck proposed that the energy of electromagnetic radiation (such as light) is not continuous but quantized. He introduced the idea of energy packets called "quanta" or "photons," where each quantum carries an energy proportional to its frequency (E = hf), and h is Planck's constant (approximately 6.626 x 10^-34 joule-seconds).

Oscillators and Resonators: Planck considered the blackbody as an ensemble of oscillators (charged particles) that can only emit or absorb energy in discrete multiples of hf. This postulate successfully explained the observed spectrum of blackbody radiation, which classical theories failed to account for.

Discrete Energy Levels: The energy levels of these oscillators are quantized, and they can only change energy states in discrete steps by absorbing or emitting whole-number multiples of hf.

Planck's quantum theory marked a significant departure from classical physics and paved the way for the development of quantum mechanics, eventually leading to a revolution in our understanding of the behavior of particles and waves at the atomic and subatomic scales.

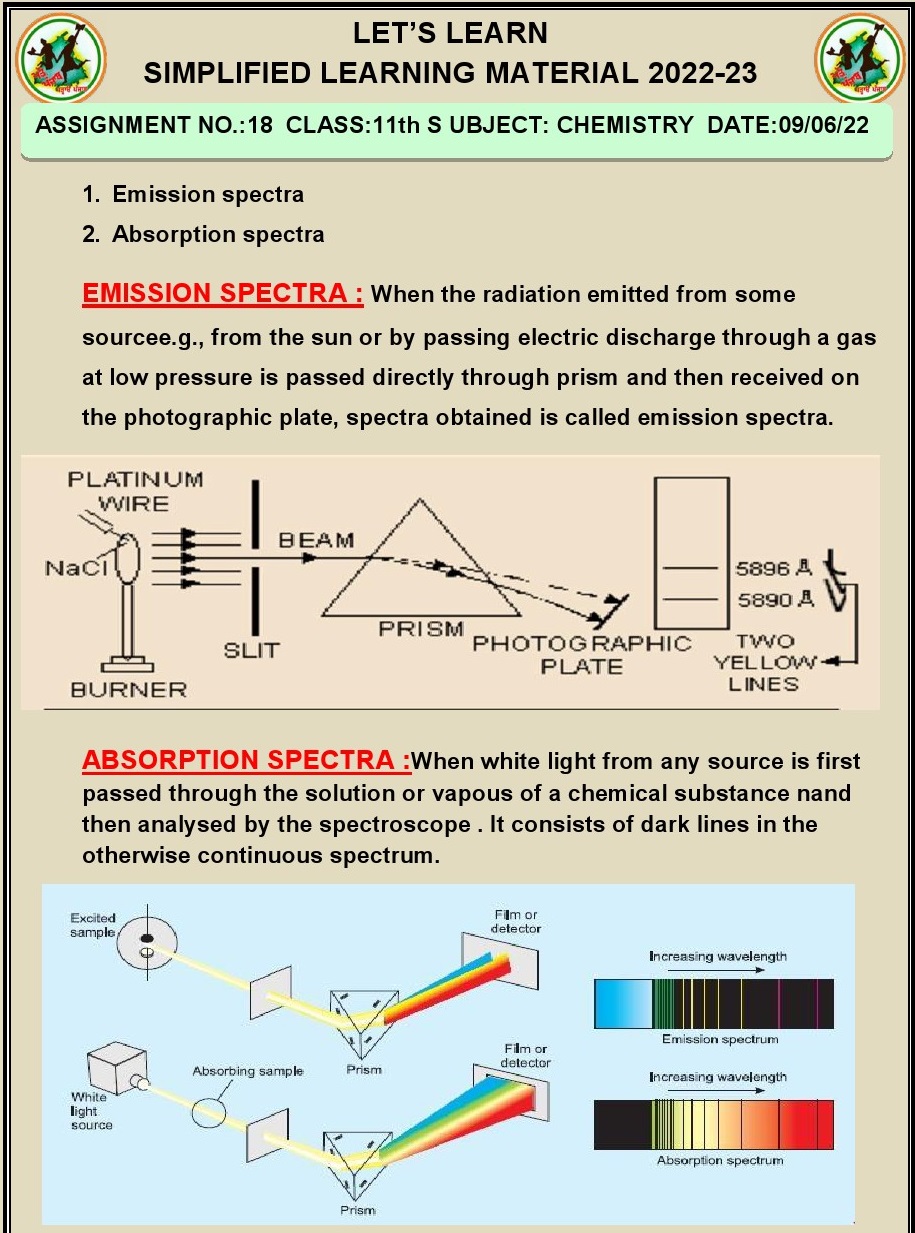
Q.8.What is emission spectra Explain different types of emission spectra?

Ans. Emission spectra refer to the characteristic patterns of electromagnetic radiation (light) emitted by atoms or molecules when they transition from higher energy states to lower energy states. These transitions occur when excited electrons within the atom or molecule lose energy and return to their ground state.

There are three types of emission spectra:

Continuous Spectrum: A continuous spectrum is produced by a source of light that emits a continuous range of wavelengths without any gaps or lines. Incandescent light bulbs and white sunlight are examples of sources that produce continuous spectra.

Line Spectrum (or Bright-line Spectrum): A line spectrum consists of discrete, bright lines of different colors separated by dark spaces. Each line corresponds to a specific wavelength of light emitted when excited electrons in an atom or molecule return to lower energy levels. These lines are characteristic of the elements or molecules emitting the light and are used in spectroscopy for identification and analysis.

Band Spectrum (or Absorption Spectrum): A band spectrum shows a series of continuous bands of colors with dark spaces or gaps between them. These spectra result from the absorption of specific wavelengths of light by an atom or molecule, where certain energy levels are allowed, and others are forbidden. The bands appear when light passes through a medium, such as a gas, that absorbs specific wavelengths.

The study of emission spectra is crucial in understanding atomic and molecular structures and has applications in various fields, including astronomy, chemistry, and physics. It provides valuable information about the energy levels and transitions of electrons within atoms and molecules, leading to a deeper understanding of the properties and behavior of matter at the quantum level.

Q.9. Write at least four differences between orbit and orbital?

Ans. Definition:

Orbit: An orbit refers to the well-defined, fixed path followed by an electron around the nucleus in the Bohr model of the atom.

Orbital: An orbital is a probability distribution or region in space where there is a high probability of finding an electron in the quantum mechanical model of the atom.

Nature:

Orbit: In the Bohr model, orbits are considered as specific, circular paths with a fixed radius and energy for electrons in an atom.

Orbital: In the quantum mechanical model, orbitals are described as three-dimensional regions around the nucleus, characterized by specific shapes and energy levels.

Uncertainty:

Orbit: Orbits were considered to be precisely defined paths with no uncertainty in the electron's position or momentum.

Orbital: Orbital describes the probability of finding an electron at a particular location, so there is inherent uncertainty in its exact position.

Compatibility with Quantum Mechanics:

Orbit: The Bohr model's concept of orbits was based on classical physics and was later found to be incompatible with the principles of quantum mechanics.

Orbital: Orbitals are a fundamental concept in quantum mechanics and provide a more accurate description of the electron's behavior in atoms, incorporating wave-like properties.

Q.10. Why is the energy of electron in an atom negative?

Ans. In the context of quantum mechanics and the Schrödinger equation, the energy of an electron in an atom is negative when it is bound to the nucleus. This negativity arises from the nature of the mathematical solutions to the Schrödinger equation, which describe the behavior of electrons as wave functions.

The negative energy indicates that the electron's energy is lower (more stable) in the bound state within the atom compared to being completely free and far away from the nucleus. When an electron is bound to the nucleus, it is subject to the attractive force of the positively charged protons in the nucleus, and this attractive force lowers the electron's potential energy.

In quantum mechanics, the absolute value of the energy itself is not as important as the differences in energy levels. Negative energy merely represents that the electron is in a bound state, whereas positive energy values typically refer to free electrons or those in higher energy states. The concept of negative energy is a mathematical result and plays a crucial role in understanding the stability and behavior of electrons within atoms.

 

 

 

 

 

 

 

 

 

 

 

 

Unit 2 Structure Of Atom